题目内容
甲、乙两人独立解出某一道数学题的概率相同,已知该题被甲或乙解出的概率为0.36.求:
(1)甲独立解出该题的概率;
(2)解出该题的人数ξ的数学期望.
(1)甲独立解出该题的概率;
(2)解出该题的人数ξ的数学期望.
分析:(1)设甲乙单独解出概率为P,则单独解不出的概率为(1-P),此题没被解出的概率是1-0.36=0.64,从而可建立方程,即可求得甲独立解出该题的概率;
(2)由题意,解出该题的人数ξ的可能取值为0、1、2,求出相应的概率,可得ξ的概率分布列,即可求得Eξ的值.
(2)由题意,解出该题的人数ξ的可能取值为0、1、2,求出相应的概率,可得ξ的概率分布列,即可求得Eξ的值.
解答:解:(1)设甲乙单独解出概率为P,则单独解不出的概率为(1-P),此题没被解出的概率是1-0.36=0.64
所以都解不出的概率(1-P)2=0.64,p=0.2,即甲独立解出该题的概率为0.2;
(2)由题意,解出该题的人数ξ的可能取值为0、1、2,且
P(ξ=0)=(1-0.2)(1-0.2)=0.64,P(ξ=1)=(1-0.2)×0.2+0.2×(1-0.2)=0.32,P(ξ=2)=0.2×0.2=0.04,
∴ξ的概率分布列为
∴Eξ=0×0.64+1×0.32+20.04=0.4
所以都解不出的概率(1-P)2=0.64,p=0.2,即甲独立解出该题的概率为0.2;
(2)由题意,解出该题的人数ξ的可能取值为0、1、2,且
P(ξ=0)=(1-0.2)(1-0.2)=0.64,P(ξ=1)=(1-0.2)×0.2+0.2×(1-0.2)=0.32,P(ξ=2)=0.2×0.2=0.04,
∴ξ的概率分布列为
| ξ | 0 | 1 | 2 |
| P | 0.64 | 0.32 | 0.04 |
点评:本题考查离散型随机变量的概率分布列与期望,解题的关键是明确变量的取值与含义.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 的数学期望.
的数学期望. 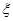 的数学期望。
的数学期望。