题目内容
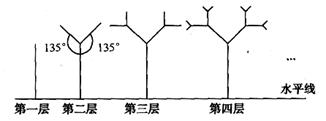
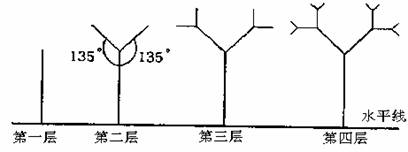
如图所示的树形图形.第一层是一条与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与该段均成1350的线段,长度为其一半;第三层按第二层的方法在每一线段的前端生成两条线段;重复前面的作法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度.
(Ⅰ)求第三层及第四层树形图的高度H3,H4;
(Ⅱ)求第n层树形图的高度Hn;
(Ⅲ)若树形图的高度大于2,则称树形图为“高大”,否则称为“矮小”.显然,当![]() 时是“矮小”的,是否存在
时是“矮小”的,是否存在![]() .使得当
.使得当![]() 时,该树形图是“高大”的?
时,该树形图是“高大”的?
解:(Ⅰ)设题中树形图(从下而上)新生的各层高度所构成的数列为![]() ,
,
则![]() ,
,
所以,第三层树形图的高度![]() .
.
第四层树形图的高度![]() .
.
(Ⅱ)易知![]() ,所以第n层树形图的高度为
,所以第n层树形图的高度为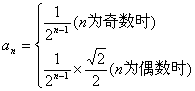 ,
,
所以,当![]() 为奇数时,第n层树形图的高度为
为奇数时,第n层树形图的高度为
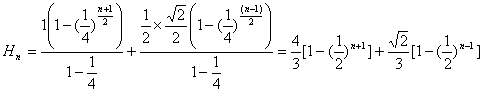 ;
;
当![]() 为偶数时,第n层树形图的高度为
为偶数时,第n层树形图的高度为
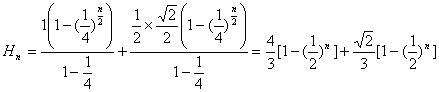 .
.
(Ⅲ)不存在.
由(Ⅱ)知,当![]() 为奇数时,
为奇数时,
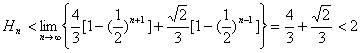 ;
;
当为偶数时,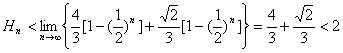 ,
,
由定义,此树形图是永远是“矮小“的.所以不存在![]() .使得当
.使得当![]() 时,该树形图是“高大”的.
时,该树形图是“高大”的.

练习册系列答案
相关题目