题目内容
已知圆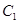 的参数方程为
的参数方程为 (
(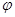 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆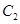 的极坐标方程为
的极坐标方程为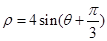 .
.
(1)将圆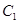 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆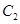 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆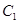 ,
,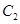 是否相交?若相交,请求出公共弦长,若不相交,请说明理由.
是否相交?若相交,请求出公共弦长,若不相交,请说明理由.
【答案】
(1) ,
, ;(2)相交,两圆的相交弦长为
;(2)相交,两圆的相交弦长为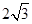 .
.
【解析】
试题分析:本题考查坐标系与参数方程、极坐标与直角坐标方程的互化,考查学生的转化能力和计算能力.第一问,利用互化公式将参数方程化为普通方程,将极坐标方程化为直角坐标方程;第二问,通过数形结合,利用几何性质求相交弦长.
试题解析:(1)由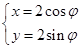 (
(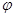 为参数),得
为参数),得 ,
,
由 ,得
,得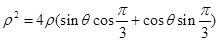 ,
,
即 ,整理得,
,整理得, .
5分
.
5分
(2)由于圆 表示圆心为原点,半径为2的圆,圆
表示圆心为原点,半径为2的圆,圆 表示圆心为
表示圆心为 ,半径为2的圆,
,半径为2的圆,
又圆 的圆心
的圆心 在圆
在圆 上,由几何性质易知,两圆的相交弦长为
上,由几何性质易知,两圆的相交弦长为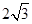 .
10分
.
10分
考点:1.参数方程与普通方程的互化;2.极坐标方程与直角坐标方程的互化;3.相交弦问题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
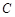 的参数方程为
的参数方程为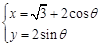 (
( 为参数),若
为参数),若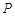 是圆
是圆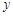 轴正半轴的交点,以坐标原点
轴正半轴的交点,以坐标原点 为极点,
为极点,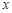 轴的正半轴为极轴建立极坐标系,则过点
轴的正半轴为极轴建立极坐标系,则过点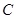 的参数方程为
的参数方程为 (
(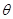 为参数),
为参数),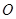 为极点、
为极点、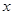 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆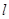 经过原点
经过原点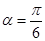 ,设
,设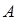 、
、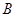 两点,求
两点,求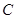 的参数方程为
的参数方程为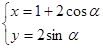 (
(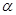 为参数).以原点为极点,
为参数).以原点为极点,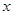 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线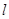 的极坐标方程为
的极坐标方程为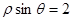 ,则直线
,则直线