题目内容
（选做题）圆内非直径的两条弦AB、CD相交于圆内一点P，已知PA=PB=4，PC=
PD，则CD=________．
10
分析：先做出辅助线，连接AC、DB，根据同弧所对的圆周角相等，证出△ACP∽△DBP，然后根据相似三角形的性质得出对应边成比例，代入数据，做出结果．
解答：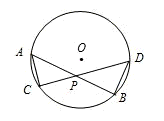
解：连接AC、BD．
∵∠A=∠D，∠C=∠B，
∴△ACP∽△DBP，
∴
=
，
∴
，
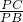∴PD2=64
∴PD=8
∴CD=PD+PC=8+2=10，
故答案为：10
点评：本题考查相似三角形的性质及相交弦定理，本题解题的关键是根据圆周角定理求出相等的角，得到三角形相似，本题是一个基础题．
分析：先做出辅助线，连接AC、DB，根据同弧所对的圆周角相等，证出△ACP∽△DBP，然后根据相似三角形的性质得出对应边成比例，代入数据，做出结果．
解答：
解：连接AC、BD．∵∠A=∠D，∠C=∠B，
∴△ACP∽△DBP，
∴
=，∴
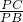，∴PD2=64
∴PD=8
∴CD=PD+PC=8+2=10，
故答案为：10
点评：本题考查相似三角形的性质及相交弦定理，本题解题的关键是根据圆周角定理求出相等的角，得到三角形相似，本题是一个基础题．
练习册系列答案
相关题目
PD，则CD= ．