题目内容
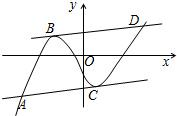 三次函数f(x)=x3+ax2+bx+c的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
三次函数f(x)=x3+ax2+bx+c的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.(1)在x=1处取得极值-2,试用c表示a和b,并求f(x)的单调区间;
(2)设点A、B、C、D的横坐标分别为xA,xB,xC,xD,求证:(xA-xB):(xB-xC):(xC-xD)=1:2:1.
分析:(1)求出f′(x)=3x2+2ax+b,由题知f′(1)=0,f(1)=-2代入即可求出a和b;然后令导函数=0求出驻点,分区间讨论出函数的增减性区间;
(2)设出直线BD的解析式因为D为交点,把D点坐标代入得到xD+2xB+a=0,同理有xA+2xC+a=0,有xA+2xC+a=0,由于AC平行于BD,因此f′(xB)=f′(xC),得到xB+xC=-
,分别求出得比值为1:2:1即可.
(2)设出直线BD的解析式因为D为交点,把D点坐标代入得到xD+2xB+a=0,同理有xA+2xC+a=0,有xA+2xC+a=0,由于AC平行于BD,因此f′(xB)=f′(xC),得到xB+xC=-
| 2a |
| 3 |
解答:解:(1)f'(x)=3x2+2ax+b,
依题意有
?
从而f′(x)=3x2+2cx-(2c+3)=0=(3x+(2c+3))(x-1),
令f′(x)=0有x=1或x=-
由于f(x)在x=1处取得极值,
因此-
≠1,得到c≠-31若-
>1,
即c<-3,则当x∈(-∞,1)或x∈(-
,+∞)时,f′(x)>0,
当x∈(1,-
)时,f′(x)<0,
因此f(x)的单调递增区间为(-∞,1)和(-
,+∞),单调递减区间为(1,-
);
若-
<1,即c>-3,
则当x∈(-∞,-
)或x∈(1,+∞)时,f′(x)>0,
当x∈(-
,1)时,f′(x)<0,
因此f(x)的单调递增区间为(-∞,-
)和(1,+∞),单调递减区间为(-
,1).
(2)设直线BD的方程为y=f′(xB)(x-xB)+f(xB)因为D点在直线上又在曲线上,
所以f(xD)=f′(xB)(xD-xB)+f(xB)
即(xD3+axD2+bxD+c)-(xB3+axB2+bxB+c)=(3xB2+2axB+b)(xD-xB)
得到:xD2+xDxB-2xB2+axD-axB=0从而xD+2xB+a=0,
同理有xA+2xC+a=0,由于AC平行于BD,
因此f′(xB)=f′(xC),
得到xB+xC=-
进一步化简可以得到xA+xD=xB+xC=-
,
从而xA-xB=xC-xD
又(xA-xB)+(xC-xD)=(xB-xC),
因此(xA-xB):(xB-xC):(xC-xD)=1:2:1
依题意有
|
|
从而f′(x)=3x2+2cx-(2c+3)=0=(3x+(2c+3))(x-1),
令f′(x)=0有x=1或x=-
| 2c+3 |
| 3 |
由于f(x)在x=1处取得极值,
因此-
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
即c<-3,则当x∈(-∞,1)或x∈(-
| 2c+3 |
| 3 |
当x∈(1,-
| 2c+3 |
| 3 |
因此f(x)的单调递增区间为(-∞,1)和(-
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
若-
| 2c+3 |
| 3 |
则当x∈(-∞,-
| 2c+3 |
| 3 |
当x∈(-
| 2c+3 |
| 3 |
因此f(x)的单调递增区间为(-∞,-
| 2c+3 |
| 3 |
| 2c+3 |
| 3 |
(2)设直线BD的方程为y=f′(xB)(x-xB)+f(xB)因为D点在直线上又在曲线上,
所以f(xD)=f′(xB)(xD-xB)+f(xB)
即(xD3+axD2+bxD+c)-(xB3+axB2+bxB+c)=(3xB2+2axB+b)(xD-xB)
得到:xD2+xDxB-2xB2+axD-axB=0从而xD+2xB+a=0,
同理有xA+2xC+a=0,由于AC平行于BD,
因此f′(xB)=f′(xC),
得到xB+xC=-
| 2a |
| 3 |
进一步化简可以得到xA+xD=xB+xC=-
| 2a |
| 3 |
从而xA-xB=xC-xD
又(xA-xB)+(xC-xD)=(xB-xC),
因此(xA-xB):(xB-xC):(xC-xD)=1:2:1
点评:考查学生利用导数研究函数极值,研究函数单调性的能力,函数与方程的灵活运用能力.

练习册系列答案
相关题目
 ,请你根据上面探究结果,解答以下问题
,请你根据上面探究结果,解答以下问题 x3-
x3- x2+3x-
x2+3x-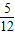 的对称中心为 ;
的对称中心为 ; +…+f(
+…+f(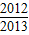 )= .
)= .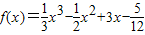 ,请你根据上面探究结果,解答以下问题
,请你根据上面探究结果,解答以下问题 x3-
x3- x2+3x-
x2+3x-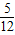 的对称中心为 ;
的对称中心为 ;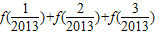 +…+f(
+…+f(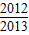 )= .
)= .