题目内容
已知圆A:(x+2)2+y2=32,圆P过定点B(2,0)且与圆A内切.
(1)求圆心P的轨迹方程C;
(2)过Q(0,3)作直线l交P的轨迹C于M、N两点,O为原点.当△MON面积最大时,求此时直线l的斜率.
解:(1)由题意,两圆相内切,故|PA|=4 -|PB|,即|PA|+|PB|=4
-|PB|,即|PA|+|PB|=4 .
.
又∵AB=4<4
∴动圆的圆心P的轨迹为以A、B为焦点,长轴长为4 的椭圆.
的椭圆.
动点P的轨迹方程为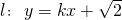 .
.
(2)解:设M(x1,y1),N(x2,y2),l:x=m(y-3),直线与x轴的交点为A(-3m,0)
S△MON= |OA|•|y1-y2|
|OA|•|y1-y2|
把x=m(y-3),代入椭圆方程,得m2(y-3)2+2y2-8=0,
即(m2+2)y2-6m2y-8+9m2=0,△=64-40m2>0,?m2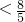
y1+y2=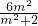 ,y1y2=
,y1y2=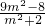 ,
,
|y1-y2|=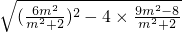 =
=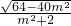
∴S△AOB= |3m|
|3m|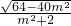 =
=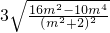 =3
=3 ,令t=
,令t=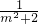 ,
,
所以S△AOB=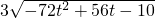 ≤
≤ ,当t=
,当t=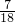 时,即m2=
时,即m2=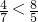 时面积取得最大值.
时面积取得最大值.
此时直线的斜率为: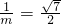 .
.
分析:(1)利用动圆P与定圆(x+2)2+y2=32相内切,以及椭圆的定义,可得动圆圆心P的轨迹M的方程;
(2)设M(x1,y1),N(x2,y2),l:y=kx+3,通过S△MON的表达式求出△OAB的面积的最大值时直线l的斜率.
点评:本题考查圆的基本知识和轨迹方程的求法以及斜率的求法,解题时要注意公式的灵活运用,此题有一定难度.
 -|PB|,即|PA|+|PB|=4
-|PB|,即|PA|+|PB|=4 .
.又∵AB=4<4

∴动圆的圆心P的轨迹为以A、B为焦点,长轴长为4
 的椭圆.
的椭圆.动点P的轨迹方程为
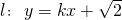 .
.(2)解:设M(x1,y1),N(x2,y2),l:x=m(y-3),直线与x轴的交点为A(-3m,0)
S△MON=
 |OA|•|y1-y2|
|OA|•|y1-y2|把x=m(y-3),代入椭圆方程,得m2(y-3)2+2y2-8=0,
即(m2+2)y2-6m2y-8+9m2=0,△=64-40m2>0,?m2
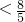
y1+y2=
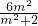 ,y1y2=
,y1y2=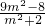 ,
,|y1-y2|=
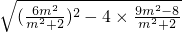 =
=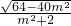
∴S△AOB=
 |3m|
|3m|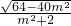 =
=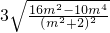 =3
=3 ,令t=
,令t=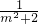 ,
,所以S△AOB=
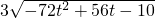 ≤
≤ ,当t=
,当t=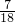 时,即m2=
时,即m2=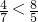 时面积取得最大值.
时面积取得最大值.此时直线的斜率为:
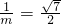 .
.分析:(1)利用动圆P与定圆(x+2)2+y2=32相内切,以及椭圆的定义,可得动圆圆心P的轨迹M的方程;
(2)设M(x1,y1),N(x2,y2),l:y=kx+3,通过S△MON的表达式求出△OAB的面积的最大值时直线l的斜率.
点评:本题考查圆的基本知识和轨迹方程的求法以及斜率的求法,解题时要注意公式的灵活运用,此题有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目