题目内容
已知m、n、s、t∈R+，m+n=2，
+
=9其中m、n是常数，且s+t的最小值是
，满足条件的点（m、n）是圆（x-2）2+（y-2）2=4中一弦的中点，则此弦所在的直线方程为
| m |
| s |
| n |
| t |
| 4 |
| 9 |
x+y-2=0
x+y-2=0
．分析：根据s+t的最小值是
，根据均值不等式求得(s+t)(
+
)的最下值，进而求得此时的m和n，进而根据圆心坐标求得弦所在的直线的斜率，最后利用点斜式求得直线的方程．
| 4 |
| 9 |
| m |
| s |
| n |
| t |
解答：解：∵(s+t)(
+
)=m+n+
+
≥m+n+2
，（m=n时取等号）
∴m+n+2
=4，
∴mn=1，得m=n=1得点（1，1），
∵已知圆的圆心为（2，2），
∴所求之弦的斜率为-
=-1，
从而弦方程为x+y-2=0．
故答案为：x+y-2=0
| m |
| s |
| n |
| t |
| tm |
| s |
| sn |
| t |
| mn |
∴m+n+2
| mn |
∴mn=1，得m=n=1得点（1，1），
∵已知圆的圆心为（2，2），
∴所求之弦的斜率为-
| 1-2 |
| 1-2 |
从而弦方程为x+y-2=0．
故答案为：x+y-2=0
点评：本题考查基本不等式、圆、直线方程等相关知识，其中整体代换是解题技巧，数形结合是解题思想解题探究．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
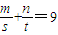，其中m、n是常数，当s+t取最小值
时，m、n对应的点（m，n）是双曲线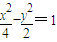
一条弦的中点，则此弦所在的直线方程为 ．