题目内容
(本小题满分12分)
在如图所示的四棱锥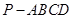 中,已知 PA⊥平面ABCD,
中,已知 PA⊥平面ABCD, 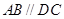 ,
, 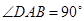 ,
,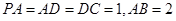 ,
, 为
为 的中点.
的中点.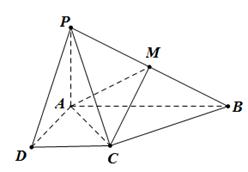
(1)求证:MC∥平面PAD;
(2)求直线MC与平面PAC所成角的余弦值;
(3)求二面角 的平面角的正切值.
的平面角的正切值.
(1)根据中位线性质,得到EM//AB,且EM= 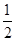 AB. 又因为
AB. 又因为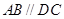 ,且
,且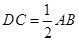 ,所以EM//DC,且EM=DC ∴四边形DCME为平行四边形, 则MC∥DE,
,所以EM//DC,且EM=DC ∴四边形DCME为平行四边形, 则MC∥DE,
(2)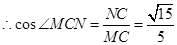 (3)
(3) 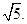
解析试题分析:(1 )如图,取PA的中点E,连接ME,DE,∵M为PB的中点,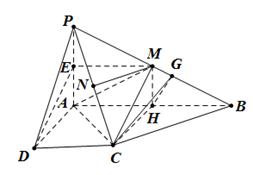
∴EM//AB,且EM= 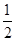 AB. 又∵
AB. 又∵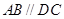 ,且
,且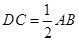 ,
,
∴EM//DC,且EM=DC ∴四边形DCME为平行四边形,
则MC∥DE,又 平面PAD,
平面PAD, 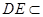 平面PAD
平面PAD
所以MC∥平面PAD
(2)取PC中点N,则MN∥BC,∵PA⊥平面ABCD,∴PA⊥BC ,
又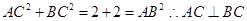 ,∴BC⊥平面PAC,
,∴BC⊥平面PAC,
则MN⊥平面PAC所以,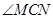 为直线MC与平面PAC所成角,
为直线MC与平面PAC所成角,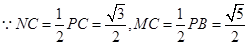
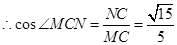
(3)取AB的中点H,连接CH,则由题意得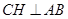
又PA⊥平面ABCD,所以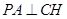 ,则
,则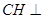 平面PAB.
平面PAB.
所以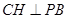 ,过H作
,过H作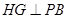 于G,连接CG,则
于G,连接CG,则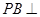 平面CGH,所以
平面CGH,所以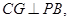
则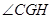 为二面角
为二面角 的平面角.
的平面角. 
则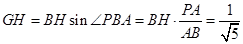 ,
,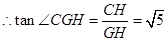
故二面角 的平面角的正切值为
的平面角的正切值为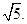
考点:本试题考查了线面角和二面角的求解运用。
点评:解决该试题的关键是能利用线面角和二面角的定义,准确的表示角,借助于三角形的知识来求解得到,也可以建立空间直角坐标系来运用空间向量法来得到求解,属于中档题。

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 中,
中, ,
, ,
, ,
, ,
, , 点
, 点 ,
, 分别在棱
分别在棱 上,且
上,且 ,
,
 平面PAC
平面PAC 的中点时,求
的中点时,求 与平面
与平面 所成的角的正弦值;
所成的角的正弦值; 为直二面角?并说明理由.
为直二面角?并说明理由. 的底面为菱形,且
的底面为菱形,且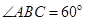 ,
,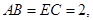
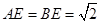 ,
,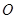 为
为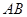 的中点.
的中点.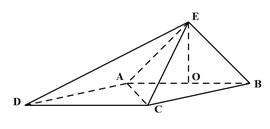
 平面
平面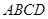 ;
; 到面
到面 的距离.
的距离.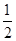 PD.
PD.
 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点,  ,且
,且 .将梯形
.将梯形 折成直二面角
折成直二面角 ,如图2所示.
,如图2所示.
 平面
平面 ;
; 关于点
关于点 的对称点为
的对称点为 ,点
,点 在
在 所在平面内,且直线
所在平面内,且直线 与平面
与平面 所成的角为
所成的角为 ,试求出点
,试求出点 的最短距离.
的最短距离. 所在平面,且PA=AB=AC.
所在平面,且PA=AB=AC.
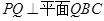 ,求二面角Q-PB-A的余弦值。
,求二面角Q-PB-A的余弦值。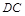 ⊥平面
⊥平面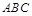 ,
,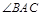 =90°,
=90°,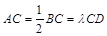 ,点
,点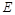 在
在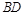 上,点E在BC上的射影为F,且
上,点E在BC上的射影为F,且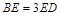 .
.
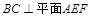 ;
;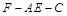 的大小为45°,求
的大小为45°,求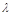 的值.
的值.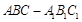 中,
中, ,
,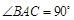 .
.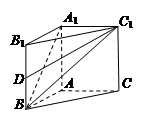
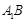 与
与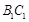 所成的角为
所成的角为 ,求棱柱的高;
,求棱柱的高;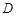 是
是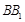 的中点,
的中点,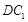 与平面
与平面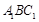 所成的角为
所成的角为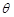 ,当棱柱的高变化时,求
,当棱柱的高变化时,求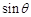 的最大值.
的最大值.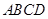 ⊥平面
⊥平面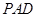 ,
, 是直角三角形,
是直角三角形,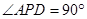 ,四边形
,四边形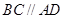 ,
,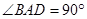 ,
, ,且
,且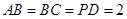 ,
,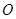 是
是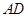 的中点,
的中点,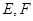 分别是
分别是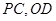 的中点.
的中点. 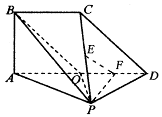
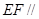 平面
平面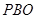 ;
;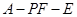 的正切值.
的正切值.