Question

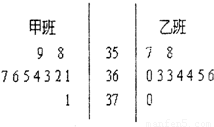
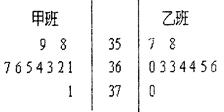
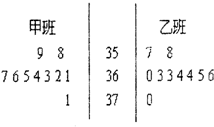为检测学生的体温状况，随机抽取甲，乙两个班各10名同学，测量他们的体温（单位0.1摄氏度）获得体温数据的茎叶图，如图所示．
（1）计算乙班的样本平均数，方差；
（2）现在从甲班中随机抽取两名体温不低于36.5摄氏度的同学，求体温为37.1摄氏度的同学被抽到的概率．

Answer 1

分析：（1）根据茎叶图读出数据，由平均数、方差的计算公式，计算可得答案；
（2）根据茎叶图可得，甲班中有一人体温为37.1摄氏度，记为a，有3名同学体温36.5到37.1之间，记为b、c、d，其；用列举法列举从这四人中抽取两人的情况数目以及a被抽到的情况数目，由概率的计算公式计算可得答案．

解答：解：（1）乙班的平均体温为

35.7+35.8+36.0+36.3+36.3+36.4+36.4+36.5+36.6+37

10

=36+

-0.3-0.2+0+0.3+0.3+0.4+0.4+0.5+0.6+1.0

10

=36+

3.0

10

=36.3；
方差为：

1

10

[（35.7-36.3）²+（35.8-36.3）²+（36-36.3）² +2（36.3-36.3）² +2（36.4-36.3）² +（36.5-36.3）² +（36.6-36.3）² +（37-36.3）²]=0.134；
（2）根据茎叶图可得，甲班中有一人体温为37.1摄氏度，记为a，有3名同学体温36.5到37.1之间，记为b、c、d，其；
从这四人中抽取两人的情况有：{a、b}，{a、c}，{a、d}，{b，c}，{b、d}，{c、d}，共6种；
其中a被抽到的情况有：{a、b}，{a、c}，{a、d}，共3种；
则体温为37.1摄氏度的同学被抽到的概率为

3

6

=0.5．

点评：本题考查等可能事件的概率和平均数、方差的计算，计算平均数时注意用简便方法．