题目内容
已知椭圆 (a>b>0)的离心率
(a>b>0)的离心率 ,在椭圆E上存在A,B两点关于直线l:y=x+1对称.
,在椭圆E上存在A,B两点关于直线l:y=x+1对称.(Ⅰ)现给出下列三个条件:①直线AB恰好经过椭圆E的一个焦点;②椭圆E的右焦点F到直线l的距离为
 ;③椭圆E的左、右焦点到直线l的距离之比为
;③椭圆E的左、右焦点到直线l的距离之比为 .
.试从中选择一个条件以确定椭圆E,并求出它的方程;(注:只需选择一个方案答题,如果用多种方案答题,则按第一种方案给分)
(Ⅱ)若以AB为直径的圆恰好经过椭圆E的上顶点S,求b的值.

【答案】分析:(Ⅰ)选择条件②运算量小一些,由椭圆E的右焦点F到直线l的距离为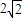 ,利用点到直线的距离公式即可得c的值,再由离心率
,利用点到直线的距离公式即可得c的值,再由离心率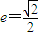 ,即可求得a值,最后由椭圆a2=b2+c2,求的b值即可得椭圆方程
,即可求得a值,最后由椭圆a2=b2+c2,求的b值即可得椭圆方程
(Ⅱ)先由离心率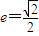 ,得a2=2b2,将椭圆方程化为
,得a2=2b2,将椭圆方程化为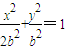 ,再由椭圆E上存在A,B两点关于直线l:y=x+1对称,知AB的中点(
,再由椭圆E上存在A,B两点关于直线l:y=x+1对称,知AB的中点(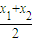 ,
,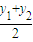 )在直线:y=x+1上,联立直线AB和椭圆方程,利用韦达定理列方程可得m的值,最后利用以AB为直径的圆恰好经过椭圆E的上顶点S(0,b),,即AS⊥BS,即
)在直线:y=x+1上,联立直线AB和椭圆方程,利用韦达定理列方程可得m的值,最后利用以AB为直径的圆恰好经过椭圆E的上顶点S(0,b),,即AS⊥BS,即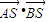 =0,利用韦达定理列方程即可得b的值
=0,利用韦达定理列方程即可得b的值
解答:解:(Ⅰ)选择条件②,∵椭圆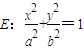 (a>b>0)的离心率
(a>b>0)的离心率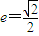 ,
,
∴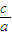 =
=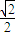 ,椭圆的右焦点坐标为(c,0)
,椭圆的右焦点坐标为(c,0)
∵右焦点F到直线l的距离为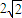 ,
,
∴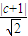 =
=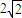 ,
,
∴c=3,a=3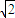
∵a2=b2+c2,
∴b2=9
∴椭圆E的方程为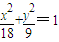
(Ⅱ)∵离心率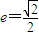
∴a2=2b2
∵A,B两点关于直线l:y=x+1对称,
∴直线AB的斜率为-1,设直线AB的方程为y=-x+m,代入椭圆方程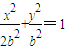 得:(3b2)x2-4mb2x+2b2m2-2b4=0
得:(3b2)x2-4mb2x+2b2m2-2b4=0
∴△>0时,x1+x2=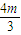 ,x1x2=
,x1x2=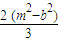
依题意,设A(x1,y1),B(x2,y2),
∵椭圆E上存在A,B两点关于直线l:y=x+1对称,
∴AB的中点(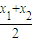 ,
,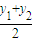 )在直线:y=x+1上
)在直线:y=x+1上
∵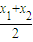 =
=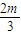 ,
,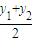 =
=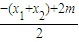 =
=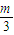 ,
,
∴m=-3
∵椭圆E的上顶点S(0,b),以AB为直径的圆恰好经过椭圆E的上顶点S,即AS⊥BS,即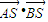 =0,即(-x1,b-y1)•(-x2,b-y2)=0
=0,即(-x1,b-y1)•(-x2,b-y2)=0
∴x1x2+(b-y1)(b-y2)=x1x2+y1y2-b(y1+y2)+b2=2x1x2+(b+3)(x1+x2)+9+6b+b2=0
∴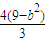 -4(b+3))+9+6b+b2=0,解得b=9,b=-3(舍去)
-4(b+3))+9+6b+b2=0,解得b=9,b=-3(舍去)
∴b=9
点评:本题考察了椭圆的标准方程及几何性质,直线与椭圆的位置关系,解题时要认真体会韦达定理在解决直线与圆锥曲线问题中的重要应用.
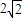 ,利用点到直线的距离公式即可得c的值,再由离心率
,利用点到直线的距离公式即可得c的值,再由离心率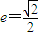 ,即可求得a值,最后由椭圆a2=b2+c2,求的b值即可得椭圆方程
,即可求得a值,最后由椭圆a2=b2+c2,求的b值即可得椭圆方程(Ⅱ)先由离心率
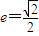 ,得a2=2b2,将椭圆方程化为
,得a2=2b2,将椭圆方程化为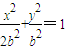 ,再由椭圆E上存在A,B两点关于直线l:y=x+1对称,知AB的中点(
,再由椭圆E上存在A,B两点关于直线l:y=x+1对称,知AB的中点(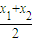 ,
,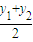 )在直线:y=x+1上,联立直线AB和椭圆方程,利用韦达定理列方程可得m的值,最后利用以AB为直径的圆恰好经过椭圆E的上顶点S(0,b),,即AS⊥BS,即
)在直线:y=x+1上,联立直线AB和椭圆方程,利用韦达定理列方程可得m的值,最后利用以AB为直径的圆恰好经过椭圆E的上顶点S(0,b),,即AS⊥BS,即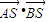 =0,利用韦达定理列方程即可得b的值
=0,利用韦达定理列方程即可得b的值解答:解:(Ⅰ)选择条件②,∵椭圆
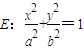 (a>b>0)的离心率
(a>b>0)的离心率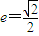 ,
,∴
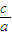 =
=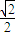 ,椭圆的右焦点坐标为(c,0)
,椭圆的右焦点坐标为(c,0)∵右焦点F到直线l的距离为
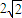 ,
,∴
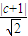 =
=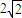 ,
,∴c=3,a=3
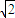
∵a2=b2+c2,
∴b2=9
∴椭圆E的方程为
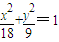
(Ⅱ)∵离心率
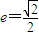
∴a2=2b2
∵A,B两点关于直线l:y=x+1对称,
∴直线AB的斜率为-1,设直线AB的方程为y=-x+m,代入椭圆方程
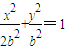 得:(3b2)x2-4mb2x+2b2m2-2b4=0
得:(3b2)x2-4mb2x+2b2m2-2b4=0∴△>0时,x1+x2=
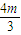 ,x1x2=
,x1x2=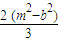
依题意,设A(x1,y1),B(x2,y2),
∵椭圆E上存在A,B两点关于直线l:y=x+1对称,
∴AB的中点(
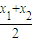 ,
,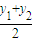 )在直线:y=x+1上
)在直线:y=x+1上∵
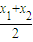 =
=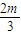 ,
,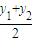 =
=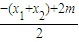 =
=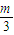 ,
,∴m=-3
∵椭圆E的上顶点S(0,b),以AB为直径的圆恰好经过椭圆E的上顶点S,即AS⊥BS,即
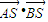 =0,即(-x1,b-y1)•(-x2,b-y2)=0
=0,即(-x1,b-y1)•(-x2,b-y2)=0∴x1x2+(b-y1)(b-y2)=x1x2+y1y2-b(y1+y2)+b2=2x1x2+(b+3)(x1+x2)+9+6b+b2=0
∴
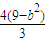 -4(b+3))+9+6b+b2=0,解得b=9,b=-3(舍去)
-4(b+3))+9+6b+b2=0,解得b=9,b=-3(舍去)∴b=9
点评:本题考察了椭圆的标准方程及几何性质,直线与椭圆的位置关系,解题时要认真体会韦达定理在解决直线与圆锥曲线问题中的重要应用.

练习册系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.