题目内容
(2011•顺义区二模)已知椭圆C的左,右焦点坐标分别为F1(-
,0),F2(
,0),离心率是
.椭圆C的左,右顶点分别记为A,B.点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线l:x=-
分别交于M,N两点.
(1)求椭圆C的方程;
(2)求线段MN长度的最小值;
(3)当线段MN的长度最小时,在椭圆C上的T满足:△TSA的面积为
.试确定点T的个数.
| 3 |
| 3 |
| ||
| 2 |
| 10 |
| 3 |
(1)求椭圆C的方程;
(2)求线段MN长度的最小值;
(3)当线段MN的长度最小时,在椭圆C上的T满足:△TSA的面积为
| 1 |
| 5 |
分析:(1)因为已知离心率及焦点坐标,故可解出椭圆的a,c及b,即知椭圆的长半轴长与短半轴长,依定义写出椭圆的方程即可.
(2)引入直线AS的斜率k,用点斜式写出直线AS的方程,与l的方程联立求出点M的坐标,以及点S的坐标,又点B的坐标已知,故可解 出直线SB的方程,亦用参数k表示的方程,使其与直线l联立,求出点N的坐标,故线段MN的长度可以表示成直线AS的斜率k的函数,根据其形式选择单调性法或者基本不等式法求最值,本题适合用基本不等式求最值.
(3)在上一问的基础上求出参数k,则直线SB的方程已知,可求出线段AB的长度,若使面积为
,只须点T到直线BS的距离为
即可,由此问题转化为研究与直线SB平行且距离为
的直线与椭圆的交点个数问题即得.
(2)引入直线AS的斜率k,用点斜式写出直线AS的方程,与l的方程联立求出点M的坐标,以及点S的坐标,又点B的坐标已知,故可解 出直线SB的方程,亦用参数k表示的方程,使其与直线l联立,求出点N的坐标,故线段MN的长度可以表示成直线AS的斜率k的函数,根据其形式选择单调性法或者基本不等式法求最值,本题适合用基本不等式求最值.
(3)在上一问的基础上求出参数k,则直线SB的方程已知,可求出线段AB的长度,若使面积为
| 1 |
| 5 |
| ||
| 4 |
| ||
| 4 |
解答: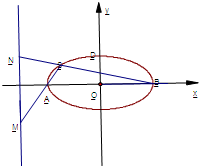 解:(1)因为
解:(1)因为
=
,且c=
,所以a=2,b=
=1
所以椭圆C的方程为
+y2=1
(2 ) 易知椭圆C的左,右顶点坐标为A(-2,0),B(2,0),直线AS的斜率k显然存在,且k>0
故可设直线AS的方程为y=k(x+2),从而M(-
,-
k)
由{,
得(1+4k2)x2+16k2x+16k2-4=0
设S(x1,y1),则(-2)x1=
,得x1=
从而y1=
,即S(
,
)
又B(2,0),故直线BS的方程为y=-
(x-2)
由
得
,
所以N(-
,
),故|MN|=|
+
|
又k>0,所以|MN|=
+
≥2
=
当且仅当
=
时,即k=1时等号成立
所以k=1时,线段MN的长度取最小值
…..(9分)
(3)由(2)知,当线段MN的长度取最小值时,k=1
此时AS的方程为x-y+2=0,S(-
,
),
所以|AS|=
,要使△TSA的面积为
,
只需点T到直线AS的距离等于
,
所以点T在平行于AS且与AS距离等于
的直线l′上
设l′:x-y+t=0,则由
=
,解得t=
或t=
1当t=
2时,由
得5x2+12x+5=607
由于△=44>0,故直线l′与椭圆C有两个不同交点
②t=
时,由
得5x2+20x+21=0由于△=-20<0,
故直线l′与椭圆C没有交点
综上所求点T的个数是2.
 解:(1)因为
解:(1)因为| c |
| a |
| ||
| 2 |
| 3 |
| a2-c2 |
所以椭圆C的方程为
| x2 |
| 4 |
(2 ) 易知椭圆C的左,右顶点坐标为A(-2,0),B(2,0),直线AS的斜率k显然存在,且k>0
故可设直线AS的方程为y=k(x+2),从而M(-
| 10 |
| 3 |
| 4 |
| 3 |
由{,
|
设S(x1,y1),则(-2)x1=
| 16k2-4 |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
从而y1=
| 4k |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
又B(2,0),故直线BS的方程为y=-
| 1 |
| 4k |
由
|
|
所以N(-
| 10 |
| 3 |
| 4 |
| 3k |
| 4k |
| 3 |
| 4 |
| 3k |
又k>0,所以|MN|=
| 4k |
| 3 |
| 4 |
| 3k |
|
| 8 |
| 3 |
当且仅当
| 4k |
| 3 |
| 4 |
| 3k |
所以k=1时,线段MN的长度取最小值
| 8 |
| 3 |
(3)由(2)知,当线段MN的长度取最小值时,k=1
此时AS的方程为x-y+2=0,S(-
| 6 |
| 5 |
| 4 |
| 5 |
所以|AS|=
4
| ||
| 5 |
| 1 |
| 5 |
只需点T到直线AS的距离等于
| ||
| 4 |
所以点T在平行于AS且与AS距离等于
| ||
| 4 |
设l′:x-y+t=0,则由
| |t-2| | ||
|
| ||
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
1当t=
| 3 |
| 2 |
|
得5x2+12x+5=607
由于△=44>0,故直线l′与椭圆C有两个不同交点
②t=
| 5 |
| 2 |
|
故直线l′与椭圆C没有交点
综上所求点T的个数是2.
点评:本题是解析几何中直线与圆锥曲线位置关系中很复杂的题目,要求答题者拥有较高的探究转化能力以及对直线与圆锥曲线位置关系中特征有较好 的理解,且符号运算能力较强才能胜任此类题的解题工作,这是一个能力型的题,好题.

练习册系列答案
相关题目
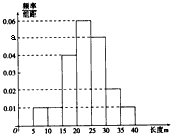 (2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=
(2011•顺义区二模)某棉纺厂为了解一批棉花的质量,从中随机抽测100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中,其频率分布直方图如图所示,由图中数据可知a=