题目内容
用符号(x]表示小于x的最大整数,如(π]=3,(-1.2]=-2.有下列命题:①若函数f(x)=(x]-x,x∈R,则f(x)的值域为[-1,0);
②若x∈(1,4),则方程x-(x]=
| 1 |
| 5 |
③若数列{an}是等差数列,则数列{(an]}也是等差数列;
④若x,y∈{
| 5 |
| 3 |
| 7 |
| 2 |
| 2 |
| 9 |
其中,所有正确命题的序号是
分析:根据题目中所给的用符号(x]表示小于x的最大整数,验证①②两个的结果得到这两个结论正确,举出一个数列推翻了③的说法,根据等可能事件的概率做出x,y∈{
,3,
},则(x]•(y]=2的概率发现正确.
| 5 |
| 3 |
| 7 |
| 2 |
解答:解:∵用符号(x]表示小于x的最大整数,
①若函数f(x)=(x]-x,x∈R,可以得到f(x)的值域为[-1,0),故①正确;
②若x∈(1,4),方程x-(x]=
变化为x=(x]+
,这样的数字有三个,故②正确;
③若数列{an}是等差数列,比如数列1.1,1.2,1.3,1.4…则数列{(an]}不是等差数列,故③不正确;
④若x,y∈{
,3,
},则(x]可能的取值是1,2,3三个数字,(x】•(y]的结果有9种,
满足乘积是2的只有2种,故概率为P=
,故④正确.
综上可知①②④正确,
故答案为:①②④
①若函数f(x)=(x]-x,x∈R,可以得到f(x)的值域为[-1,0),故①正确;
②若x∈(1,4),方程x-(x]=
| 1 |
| 5 |
| 1 |
| 5 |
③若数列{an}是等差数列,比如数列1.1,1.2,1.3,1.4…则数列{(an]}不是等差数列,故③不正确;
④若x,y∈{
| 5 |
| 3 |
| 7 |
| 2 |
满足乘积是2的只有2种,故概率为P=
| 2 |
| 9 |
综上可知①②④正确,
故答案为:①②④
点评:本题考查等可能事件的概率,考查函数的值域,考查新定义问题,考查根的存在性及根的个数的判断,考查等差数列,是一个综合题,题目考查的知识点比较多.

练习册系列答案
相关题目
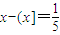 有三个根;
有三个根;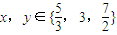 ,则(x]•(y]=2的概率为
,则(x]•(y]=2的概率为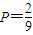 .
. 有三个根;
有三个根; ,则(x]•(y]=2的概率为
,则(x]•(y]=2的概率为 .
.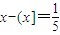 有三个根;
有三个根;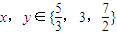 ,则(x]•(y]=2的概率为
,则(x]•(y]=2的概率为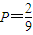 .
.