题目内容
为了加快经济的发展,某省选择A、B两城市作为龙头带动周边城市的发展,决定在A、B两城市的周边修建城际轻轨,假设10km为一个单位距离,A、B两城市相距8个单位距离,设城际轻轨所在的曲线为E,使轻轨E上的点到A、B两市的距离之和为10个单位距离.
(1)建立直角坐标系,求城际轻轨所在曲线E的方程;
(2)若要在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离,求M、N之间的距离有多少个单位距离?
(3)在A、B两城市之间有一条与AB所在直线成45°的笔直公路l,直线l与曲线E交于P,Q两点,求四边形PAQB的面积的最大值.
(1)建立直角坐标系,求城际轻轨所在曲线E的方程;
(2)若要在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离,求M、N之间的距离有多少个单位距离?
(3)在A、B两城市之间有一条与AB所在直线成45°的笔直公路l,直线l与曲线E交于P,Q两点,求四边形PAQB的面积的最大值.
(1)以AB为x轴,以AB中点为原点O建立直角坐标系.
设曲线E上点P(x,y),
∵|PA|+|PB|=10>|AB|=8
∴动点轨迹为椭圆,
且a=5,c=4,从而b=3.
∴曲线E的方程为
+
=1.(4分)
(2)∵|AM|+|AN|+|BM|+|BN|=20,
|AM|+|AN|=12,
所以|MN|=8.(8分)
(3)将y=x+t代入
+
=1,
得34y2-18ty+9t2-25×9=0.
设P(x1,y1)、Q(x2,y2),
则y1+y2=
,y1y2=
.
|y1-y2|=
=
,
S=S△ABP+S△ABQ=
AB•|y1-y2|=
,
所以当t=0时,面积最大是
,
此时直线为l:y=x.(13分)
设曲线E上点P(x,y),
∵|PA|+|PB|=10>|AB|=8
∴动点轨迹为椭圆,
且a=5,c=4,从而b=3.
∴曲线E的方程为
| x2 |
| 25 |
| y2 |
| 9 |
(2)∵|AM|+|AN|+|BM|+|BN|=20,
|AM|+|AN|=12,
所以|MN|=8.(8分)
(3)将y=x+t代入
| x2 |
| 25 |
| y2 |
| 9 |
得34y2-18ty+9t2-25×9=0.
设P(x1,y1)、Q(x2,y2),
则y1+y2=
| 9t |
| 17 |
| 9t2-25×9 |
| 34 |
|y1-y2|=
| (y1+y2)2-4y1y2 |
| 1 |
| 17 |
| 50×9×17-9×25t2 |
S=S△ABP+S△ABQ=
| 1 |
| 2 |
| 8 |
| 34 |
| 50×9×17-9×25t2 |
所以当t=0时,面积最大是
| 60 |
| 17 |
| 34 |
此时直线为l:y=x.(13分)

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.
个单位距离,城际快速通道所在的曲线为E,使快速通道E上的点到两区的距离之和为4个单位距离.
 的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足
的笔直公路l与曲线E交于P,Q两点,同时在曲线E上建一个加油站M(横坐标为负值)满足 ,求
,求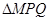 面积的最大值.
面积的最大值. 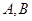 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在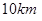 为一个单位距离,
为一个单位距离,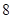 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为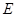 ,使轻轨
,使轻轨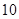 个单位距离,
个单位距离,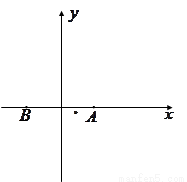
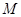 与一个收费站
与一个收费站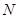 ,使
,使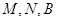 三点在一条直线上,并且
三点在一条直线上,并且 个单位距离,求
个单位距离,求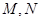 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?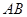 所在直线成
所在直线成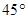 的笔直公路
的笔直公路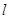 ,直线
,直线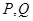 两点,求四边形
两点,求四边形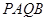 的面积的最大值.
的面积的最大值.