题目内容
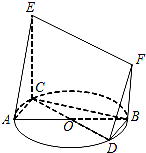 (2013•徐州三模)如图,AB,CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE.求证:
(2013•徐州三模)如图,AB,CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE.求证:(1)平面BCEF⊥平面ACE;
(2)直线DF∥平面ACE.
分析:(1)通过证明平面ACE内的直线CE与AC都垂直BC,利用平面与平面垂直的判定定理证明平面BCEF⊥平面ACE;
(2)通过平面BDF∥平面ACE,利用DF?平面BDF,即可证明DF∥平面ACE.
(2)通过平面BDF∥平面ACE,利用DF?平面BDF,即可证明DF∥平面ACE.
解答:证明:(1)因为CE⊥圆O所在的平面,BC?圆O所在的平面,
所以CE⊥BC,…(2分)
因为AB为圆O的直径,点C在圆O上,所以AC⊥BC,…(3分)
因为AC∩CE=C,AC,CE?平面ACE,
所以BC⊥平面ACE,…(5分)
因为BC?平面BCEF,所以平面BCEF⊥平面ACE.…(7分)
(2)由(1)AC⊥BC,又因为CD为圆O的直径,
所以BD⊥BC,
因为AC,BC,BD在同一平面内,所以AC∥BD,…(9分)
因为BD?平面ACE,AC?平面ACE,所以BD∥平面ACE.…(11分)
因为BF∥CE,同理可证BF∥平面ACE,
因为BD∩BF=B,BD,BF?平面BDF,
所以平面BDF∥平面ACE,
因为DF?平面BDF,所以DF∥平面ACE.…(14分)
所以CE⊥BC,…(2分)
因为AB为圆O的直径,点C在圆O上,所以AC⊥BC,…(3分)
因为AC∩CE=C,AC,CE?平面ACE,
所以BC⊥平面ACE,…(5分)
因为BC?平面BCEF,所以平面BCEF⊥平面ACE.…(7分)
(2)由(1)AC⊥BC,又因为CD为圆O的直径,
所以BD⊥BC,
因为AC,BC,BD在同一平面内,所以AC∥BD,…(9分)
因为BD?平面ACE,AC?平面ACE,所以BD∥平面ACE.…(11分)
因为BF∥CE,同理可证BF∥平面ACE,
因为BD∩BF=B,BD,BF?平面BDF,
所以平面BDF∥平面ACE,
因为DF?平面BDF,所以DF∥平面ACE.…(14分)
点评:本题考查平面与平面垂直的判定定理,直线与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
相关题目
 (2013•徐州三模)如图是一个算法流程图,则输出的S的值是
(2013•徐州三模)如图是一个算法流程图,则输出的S的值是