题目内容
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为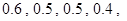 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.
(1)求同一工作日至少3人需使用设备的概率;
(2)X表示同一工作日需使用设备的人数,求X的数学期望.
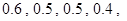 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.(1)求同一工作日至少3人需使用设备的概率;
(2)X表示同一工作日需使用设备的人数,求X的数学期望.
(1)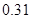 ;(2)2.
;(2)2.
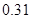 ;(2)2.
;(2)2.试题分析:(1)首先用字母表示有关的事件,
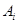 表示事件:同一工作日乙、丙恰有
表示事件:同一工作日乙、丙恰有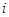 人需使用设备,
人需使用设备,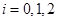 ;
;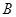 表示事件:甲需使用设备;
表示事件:甲需使用设备; 表示事件:丁需使用设备;
表示事件:丁需使用设备;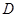 表示事件:同一工作日至少3人需使用设备.将
表示事件:同一工作日至少3人需使用设备.将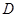 分解为互斥事件的和:
分解为互斥事件的和: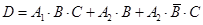 ,再利用互斥事件的概率加法公式计算
,再利用互斥事件的概率加法公式计算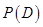 ;(2)
;(2)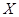 的可能取值为0,1,2,3,4.先用分解策略求分别
的可能取值为0,1,2,3,4.先用分解策略求分别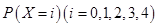 ,最后利用离散型随机变量数学期望公式求
,最后利用离散型随机变量数学期望公式求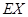 的值.
的值.试题解析:记
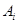 表示事件:同一工作日乙、丙恰有
表示事件:同一工作日乙、丙恰有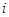 人需使用设备,
人需使用设备,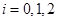 ;
;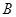 表示事件:甲需使用设备;
表示事件:甲需使用设备; 表示事件:丁需使用设备;
表示事件:丁需使用设备;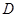 表示事件:同一工作日至少3人需使用设备.
表示事件:同一工作日至少3人需使用设备.(1)
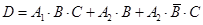 ,
,又
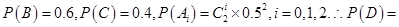
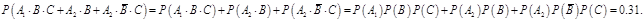 (2)
(2)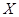 的可能取值为0,1,2,3,4.
的可能取值为0,1,2,3,4.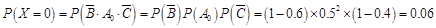 ,
,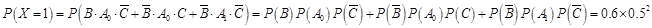
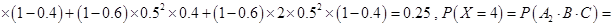
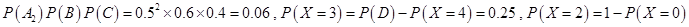
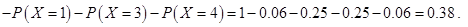 ∴数学期望
∴数学期望 考点:
考点:
练习册系列答案
相关题目
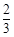 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.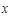 的分布列和数学期望.
的分布列和数学期望.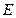 与
与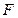 相互独立,且
相互独立,且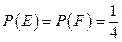 ,则
,则 的值等于
的值等于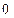
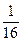
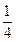

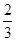 .
.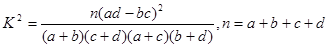
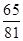 ,则事件A在1次试验中出现的概率为________.
,则事件A在1次试验中出现的概率为________.