题目内容
若不等式x2+ax+1≥0对一切 都成立,则实数a的取值范围是( )
都成立,则实数a的取值范围是( )A.(-∞,0)
B.(-∞,-2]
C.

D.[-2,+∞)
【答案】分析:对于不等式的左边,设函数f(x)=x2+ax+1,则函数f(x)在区间(0, ]上的最小值大于或等于0.然后通过二次函数的图象与性质,分别在三种情况下讨论函数f(x)的最小值大于或等于零,得到三个符合题意的实数a的取值,最后综合可得实数a的取值范围.
]上的最小值大于或等于0.然后通过二次函数的图象与性质,分别在三种情况下讨论函数f(x)的最小值大于或等于零,得到三个符合题意的实数a的取值,最后综合可得实数a的取值范围.
解答:解:∵不等式x2+ax+1≥0对一切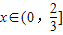 都成立,
都成立,
∴函数f(x)=x2+ax+1在区间(0, ]上的最小值大于或等于0
]上的最小值大于或等于0
而函数f(x)=x2+ax+1的图象是一条开口向上的抛物线,
其对称轴为x=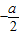 ,下面分三种情况讨论函数的最小值
,下面分三种情况讨论函数的最小值
①当x=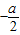 ≤0时,即a≥0时,函数f(x)在区间(0,
≤0时,即a≥0时,函数f(x)在区间(0, ]上为增函数
]上为增函数
∴函数f(x)的最小值大于f(0)=1≥0,符合题意.此时a≥0;
②当x=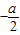 ∈(0,
∈(0, ]时,即-
]时,即- ≤a<0时,
≤a<0时,
函数f(x)的最小值为f(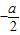 )=1-
)=1-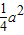 ≥0,-2≤a≤2,
≥0,-2≤a≤2,
∴- ≤a<0;
≤a<0;
③当x=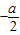 >
> 时,即a≤-
时,即a≤- 时,函数f(x)在区间(0,
时,函数f(x)在区间(0, ]上为减函数
]上为减函数
∴函数f(x)的最小值f( )=
)=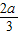 +
+ ≥0,可得a≥-
≥0,可得a≥-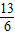
因此-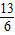 ≤a≤-
≤a≤- .
.
综上所述,得实数a的取值范围是:a≥-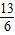
故选C
点评:本题借助于一个一元二次不等式恒成立的问题,着重考查了一元二次不等式的应用和二次函数在给定区间上的最值最值等知识点,属于中档题.
 ]上的最小值大于或等于0.然后通过二次函数的图象与性质,分别在三种情况下讨论函数f(x)的最小值大于或等于零,得到三个符合题意的实数a的取值,最后综合可得实数a的取值范围.
]上的最小值大于或等于0.然后通过二次函数的图象与性质,分别在三种情况下讨论函数f(x)的最小值大于或等于零,得到三个符合题意的实数a的取值,最后综合可得实数a的取值范围.解答:解:∵不等式x2+ax+1≥0对一切
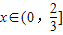 都成立,
都成立,∴函数f(x)=x2+ax+1在区间(0,
 ]上的最小值大于或等于0
]上的最小值大于或等于0而函数f(x)=x2+ax+1的图象是一条开口向上的抛物线,
其对称轴为x=
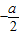 ,下面分三种情况讨论函数的最小值
,下面分三种情况讨论函数的最小值①当x=
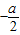 ≤0时,即a≥0时,函数f(x)在区间(0,
≤0时,即a≥0时,函数f(x)在区间(0, ]上为增函数
]上为增函数∴函数f(x)的最小值大于f(0)=1≥0,符合题意.此时a≥0;
②当x=
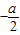 ∈(0,
∈(0, ]时,即-
]时,即- ≤a<0时,
≤a<0时,函数f(x)的最小值为f(
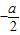 )=1-
)=1-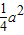 ≥0,-2≤a≤2,
≥0,-2≤a≤2,∴-
 ≤a<0;
≤a<0;③当x=
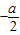 >
> 时,即a≤-
时,即a≤- 时,函数f(x)在区间(0,
时,函数f(x)在区间(0, ]上为减函数
]上为减函数∴函数f(x)的最小值f(
 )=
)=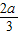 +
+ ≥0,可得a≥-
≥0,可得a≥-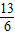
因此-
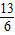 ≤a≤-
≤a≤- .
.综上所述,得实数a的取值范围是:a≥-
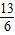
故选C
点评:本题借助于一个一元二次不等式恒成立的问题,着重考查了一元二次不等式的应用和二次函数在给定区间上的最值最值等知识点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目