题目内容
在△ABC中,D,E分别为AB,AC上的点,且DE∥BC,△ADE的面积是2cm2,梯形DBCE的面积为6cm2,则DE:BC的值为( )
A、1:
| ||
| B、1:2 | ||
| C、1:3 | ||
| D、1:4 |
分析:根据相似三角形的性质,由已知可证S△ADE:S△ABC=1:4,所以相似比是1:2,故DE:BC=1:2.
解答: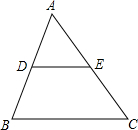 解:根据题意,△ADE的面积是2cm2,梯形DBCE的面积为6cm2,
解:根据题意,△ADE的面积是2cm2,梯形DBCE的面积为6cm2,
则S△ADE:S△ABC=1:4
∵DE∥BC
则△ADE∽△ABC
设相似比是k
则面积的比是k2=1:4
因而相似比是1:2
∴DE:BC=1:2.
故选:B.
 解:根据题意,△ADE的面积是2cm2,梯形DBCE的面积为6cm2,
解:根据题意,△ADE的面积是2cm2,梯形DBCE的面积为6cm2,则S△ADE:S△ABC=1:4
∵DE∥BC
则△ADE∽△ABC
设相似比是k
则面积的比是k2=1:4
因而相似比是1:2
∴DE:BC=1:2.
故选:B.
点评:本题主要考查了相似三角形的性质,相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
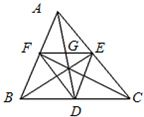 如图,在△ABC中,D、E、F分别是各边的中点,AD交EF于点G,则下列各式能表示向量
如图,在△ABC中,D、E、F分别是各边的中点,AD交EF于点G,则下列各式能表示向量| DG |
| 1 |
| 2 |
| DE |
| DF |
| 1 |
| 2 |
| CF |
| BE |
| 1 |
| 2 |
| BF |
| CE |
| 1 |
| 4 |
| AB |
| AC |
| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,D、E、F分别BC、CA、AB的中点,点M是△ABC的重心,则
+
-
等于( )
| MA |
| MB |
| MC |
A、
| ||
B、4
| ||
C、4
| ||
D、4
|
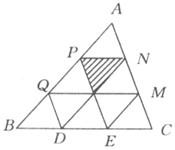 如图,在△ABC中,D、E、P、Q、M、N分别是各边的三等分点,现做投针试验,则射中阴影部分的概率是
如图,在△ABC中,D、E、P、Q、M、N分别是各边的三等分点,现做投针试验,则射中阴影部分的概率是 如图,在△ABC中,D、E为边AB的两个三等分点,
如图,在△ABC中,D、E为边AB的两个三等分点,