题目内容
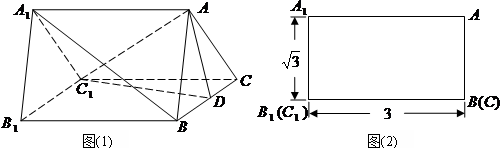
如图(1)是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的主视图如图(2).
(Ⅰ) 图(1)中垂直于平面BCC1B1的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
(Ⅱ)求正三棱柱ABC-A1B1C1的体积;
(Ⅲ)证明:A1B∥平面ADC1.
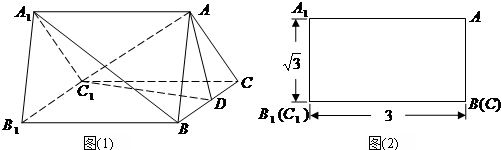
解:(Ⅰ)平面ABC、平面A1B1C1、平面AC1D.(3分)(每对1个给1分)
(Ⅱ)依题意,在正三棱柱中,AA1=3,
 ,从而BC=2.(5分),
,从而BC=2.(5分),所以正三棱柱的体积
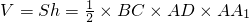 =
= .(7分).
.(7分).(Ⅲ)连接A1C,设A1C∩AC1=E,连接DE,
因为AA1C1C是正三棱柱的侧面,所以AA1C1C是矩形,E是A1C的中点,
所以DE是△A1BC的中位线,DE∥A1B.(10分)
因为DE?平面ADC1,A1B?平面ADC1,所以A1B∥平面ADC1.(12分).
分析:(I)根据直棱柱的定义,可以判断底面与侧面垂直,再结合面面垂直的判定定理,可以判断过AD的平面均与侧面BCC1B1垂直,由此即可得到答案.
(II)由已知中的主视图中标识的数据,易判断棱柱的高为3,棱柱底面的高
 ,则此计算出棱柱的底面积和高,代入即可得到棱柱的体积.
,则此计算出棱柱的底面积和高,代入即可得到棱柱的体积.(III)连接A1C,利用三角形中位线定理,易得到面内一线与面外一线平面,进而得到线面平行.
点评:本题考查的知识点是棱柱的体积公式,线面平行的判断,其中熟练掌握棱柱的几何特征,掌握线面关于的判定定理,是解答本题的关键.

练习册系列答案
相关题目
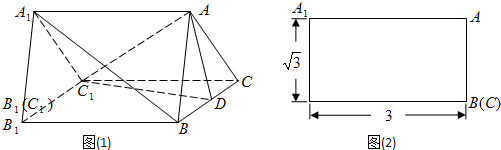
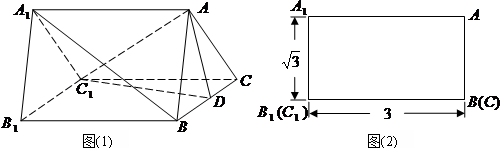
 如图(1)是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的正(主)视图如图(2)
如图(1)是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的正(主)视图如图(2)