题目内容

对任意实数x，都有（x-1）4=a0+a1（x-3）+a（x-3）2+a3（x-3）3+a4（x-3）4，则
a1+a3
a3
的值为______．
∵（x-1）4=[2+（x-3）]4=a0+a1（x-3）+a（x-3）2+a3（x-3）3+a4（x-3）4，
∴a1=
C14
•23=32，a3=
C34
•2=8，∴
a1+a3
a3
=
32+8
8
=5，
故答案为：8．
练习册系列答案
相关题目
（1+3x）（1+2x）2（1+x）3展开式中，合并同类项后，x3的系数为（　　）
A．80B．82C．84D．86
设(5x-
1
x
)n的展开式的各项系数之和为M，二项式系数之和为N，若
M
N
=32，则展开式中x2的系数为______．
若对于任意的实数x，有a0+a1（x-1）+a2（x-1）2+a3（x-1）3=x3，则a0的值为______；a2的值为______．
在（
3x
+
1
x
）20的展开式中，x的幂指数是整数的项共有（　　）
A．3项B．4项C．5项D．6项
若(1-2x)2013=a0+a1x+a2x2+…+a2013x2013(x∈R)，则
a1
2
+
a2
22
+…+
a2013
22013
的值为（　　）
A．2B．0C．-1D．-2
在（2x2-
1
3x
）8的展开式中，求：
（1）第5项的二项式系数及第五项的系数；
（2）求含x9的项．
二项式(x-
1
x
)n展开式中，仅有第五项的二项式系数最大，则其常数项为______．
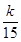设随机变量X的分布列为P(X＝k)＝(k＝1，2，3，4，5)，则P＝________.

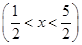违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网