题目内容
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图1).将△ABD沿着AD折起到△AB'D的位置,连接B'C(如图2).
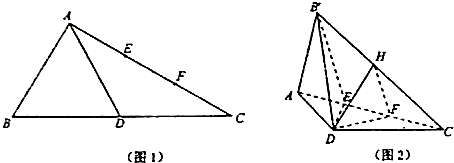
(1)若平面AB'D⊥平面AD C,求三棱锥B'-AD C的体积;
(2)记线段B'C的中点为H,平面B'ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B'E.
解:(1)在直角△ABC中,D为BC的中点,所以AD=BD=CD.
又∠B=60°,所以△ABD是等边三角形.取AD中点O,连接B'O,∴B'O⊥AD.
∵面AB'D⊥面ADC,面AB'D∩面ADC=AD,B'O?面AB'D,
∴B'O⊥面ADC.
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为BC的中点,
∴AC= ,B'O=
,B'O= ,∴
,∴ .
.
∴三棱锥B'-ADC的体积为V= .
.
(2)∵H为B'C的中点,F为CE的中点,∴HF∥B'E,
又HF?面B'ED,B'E?面B'ED,∴HF∥面B'ED,
∵HF?面HFD,面B'ED∩面HFD=l,∴HF∥l.
(3)由(1)知,B'O⊥AD.∵AE= ,
, ,∠DAC=30°,
,∠DAC=30°,
∴ =
= ,
,
∴AO2+EO2=AE2,∴AD⊥EO
又B'O?面B'EO,EO?面B'EO,B'O∩EO=O,∴AD⊥面B'EO,
又B'E?面B'EO,
∴AD⊥B'E.
分析:(1)要求三棱锥的体积,关键要确定高与底面,由于平面AB'D⊥平面AD C,则可让△ADC为底,B'到面ADC的距离为高,即要找到过B'点的AD的垂线即可;
(2)此问是要证明线线平行,又知l为平面B'ED与平面HFD的交线,故可证HF∥面B'ED,再用线面平行的性质定理即得证;
(3)要证AD⊥B'E,可用线面垂直的性质定理,即让AD垂直于B'E所在的其中一个平面即可.
点评:本题考查的是立体几何的平行与垂直的关系和空间体的体积;立体几何的平行与垂直的问题是高考的常考必考内容,除了要掌握与平行垂直相关的结论外,理科生还要注意掌握用空间向量的方法解决立体几何中的平行、垂直、空间角的问题.
又∠B=60°,所以△ABD是等边三角形.取AD中点O,连接B'O,∴B'O⊥AD.
∵面AB'D⊥面ADC,面AB'D∩面ADC=AD,B'O?面AB'D,
∴B'O⊥面ADC.
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为BC的中点,
∴AC=
 ,B'O=
,B'O= ,∴
,∴ .
.∴三棱锥B'-ADC的体积为V=
 .
.(2)∵H为B'C的中点,F为CE的中点,∴HF∥B'E,
又HF?面B'ED,B'E?面B'ED,∴HF∥面B'ED,
∵HF?面HFD,面B'ED∩面HFD=l,∴HF∥l.
(3)由(1)知,B'O⊥AD.∵AE=
 ,
, ,∠DAC=30°,
,∠DAC=30°,∴
 =
= ,
,∴AO2+EO2=AE2,∴AD⊥EO
又B'O?面B'EO,EO?面B'EO,B'O∩EO=O,∴AD⊥面B'EO,
又B'E?面B'EO,
∴AD⊥B'E.
分析:(1)要求三棱锥的体积,关键要确定高与底面,由于平面AB'D⊥平面AD C,则可让△ADC为底,B'到面ADC的距离为高,即要找到过B'点的AD的垂线即可;
(2)此问是要证明线线平行,又知l为平面B'ED与平面HFD的交线,故可证HF∥面B'ED,再用线面平行的性质定理即得证;
(3)要证AD⊥B'E,可用线面垂直的性质定理,即让AD垂直于B'E所在的其中一个平面即可.
点评:本题考查的是立体几何的平行与垂直的关系和空间体的体积;立体几何的平行与垂直的问题是高考的常考必考内容,除了要掌握与平行垂直相关的结论外,理科生还要注意掌握用空间向量的方法解决立体几何中的平行、垂直、空间角的问题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
在△ABC中
等于( )
| a+b |
| a-b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在△ABC中,
如图,在△ABC中,