题目内容
已知函数 (
(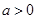 ),当
),当 时函数
时函数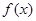 的极值为
的极值为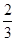 ,则
,则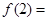 .
.
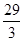
解析试题分析:∵ ,f′(x)=x2+2
,f′(x)=x2+2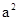 x+a,
x+a,
又∵函数 ,在x=-1处有极值为
,在x=-1处有极值为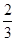 ,
,
∴f′(-1)=1-2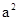 +a=0,f(-1)=
+a=0,f(-1)= -a +a2+b=
-a +a2+b=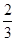
注意到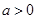 解得:a=1,b=
解得:a=1,b=
∴f(x)= x3+x2+x+
x3+x2+x+ ,故
,故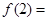
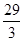 .
.
考点:本题主要考查应用导数研究函数的极值,待定系数法。
点评:中档题,本题综合考查导数计算,应用导数研究函数的极值,利用待定系数法求函数解析式。突出了对基础知识的考查,不偏不怪。

练习册系列答案
相关题目
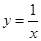 和直线
和直线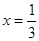 ,
,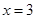 及
及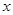 轴所围图形的面积为 .
轴所围图形的面积为 .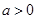 .若曲线
.若曲线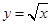 与直线
与直线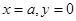 所围成封闭图形的面积为
所围成封闭图形的面积为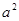 ,则
,则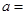 .
. 上的点
上的点 的切线方程为________________。
的切线方程为________________。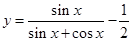 在点M(
在点M(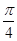 ,0)处的切线的斜率为________________.
,0)处的切线的斜率为________________. ,则
,则 ;
;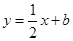 是曲线
是曲线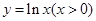 的一条切线,则实数
的一条切线,则实数 的值为
的值为 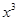 -x+3在点(1,3)处的切线方程为
-x+3在点(1,3)处的切线方程为