题目内容
(1)化简log225×log34×log59+
+(lg
-lg25)÷(-0.001)
(2)对于正数想x,y,z,t(t≠1)满足
lgx+
lgy+
lgz=1,7
log
t=106,求x6×y4×z3-t2.
| (-4)2 |
| 1 |
| 4 |
| 1 |
| 3 |
(2)对于正数想x,y,z,t(t≠1)满足
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
分析:(1)直接利用对数的运算性质求解即可.
(2)通过已知条件求出x6×y4×z3与t2的值,然后求解所求表达式的值.
(2)通过已知条件求出x6×y4×z3与t2的值,然后求解所求表达式的值.
解答:解:(1)log225×log34×log59+
+(lg
-lg25)÷(-0.001)
=8log25×log32×log53+4+(-2lg2-2lg5)÷(-0.1)
=8+4+20=32…(6分)
(2)∵
lgx+
lgy+
lgz=1∴lg
+lg
+lg
=1
∴
•
•
=10
∴x6y4z3=(
•
•
)12=1012…(8分)
∵7
log
t=106
∴t=106∴t2=1012…(10分)
∴x6y4z3-t2=0…(12分)
| (-4)2 |
| 1 |
| 4 |
| 1 |
| 3 |
=8log25×log32×log53+4+(-2lg2-2lg5)÷(-0.1)
=8+4+20=32…(6分)
(2)∵
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| x |
| 3 | y |
| 4 | z |
∴
| x |
| 3 | y |
| 4 | z |
∴x6y4z3=(
| x |
| 3 | y |
| 4 | z |
∵7
| 1 |
| 2 |
| 7 |
∴t=106∴t2=1012…(10分)
∴x6y4z3-t2=0…(12分)
点评:本题考查对数与指数的运算性质,考查整体思想与计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +(lg
+(lg -lg25)÷
-lg25)÷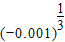
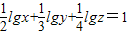 ,
,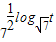 =106,求x6×y4×z3-t2.
=106,求x6×y4×z3-t2.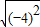 +(lg
+(lg -lg25)÷
-lg25)÷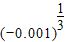
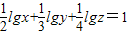 ,
,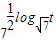 =106,求x6×y4×z3-t2.
=106,求x6×y4×z3-t2.