Question

直线y=x+3与曲线

y2

9

-

x|x|

4

=1的公共点个数为

3

．

Answer 1

分析：分x大于等于0，和x小于0两种情况去绝对值符号，可得当x≥0时，曲线

y2

9

-

x|x|

4

=1为焦点在y轴上的双曲线，当x＜0时，曲线

y2

9

-

x|x|

4

=1为焦点在y轴上的椭圆，在同一坐标系中作出直线y=x+3与曲线

y2

9

-

x|x|

4

=1的图象，就可找到交点个数．

解答：解：当x≥0时，曲线

y2

9

-

x|x|

4

=1的方程为

y2

9

-

x2

4

=1
当x＜0时，曲线

y2

9

-

x|x|

4

=1的方程为

y2

9

+

x2

4

=1，
∴曲线

y2

9

-

x|x|

4

=1的图象为右图，
在同一坐标系中作出直线y=x+3的图象，
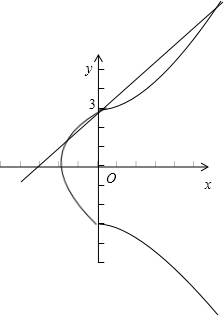
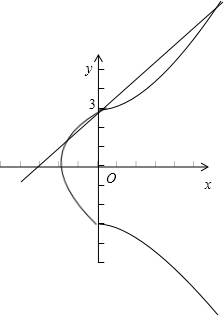
可得直线与曲线交点个数为3个．
故答案为3

点评：本题主要考查图象法求直线与曲线交点个数，关键是去绝对值符号，化简曲线方程．