题目内容
设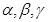 为两两不重合的平面,
为两两不重合的平面,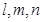 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若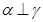 ,
,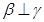 ,则
,则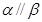 ;②若
;②若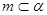 ,
,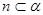 ,
,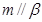 ,
,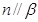 ,则
,则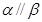 ;③若
;③若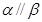 ,
,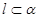 ,则
,则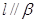 ; ④若
; ④若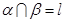 ,
,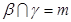 ,
,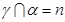 ,
,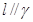 ,则
,则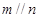 .其中真命题的个数是
.其中真命题的个数是
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:命题1中,垂直于同一个平面的两个平面可能平行也可能相交。命题2中,只有m,n相交时,则能推出面面平行。命题3中,根据面面平行的性质定理,其中一个平面的任何一条直线都平行于另一个平面。命题4中,三个平面两两相交,且交线平行,可知成立。选B.
考点:本题主要考查了立体几何中点、线、面的位置关系的运用。
点评:解决该试题的关键是熟练的运用面面平行的判定定理和性质定理和线面平行的性质定理和判定定理的综合运用问题。

练习册系列答案
相关题目
若 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,则下列命题中正确的是( )
是一条直线,则下列命题中正确的是( )
A.若 |
B.若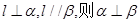 |
C.若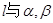 的所成角相等,则 的所成角相等,则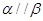 |
D.若 上有两个点到α的距离相等,则 上有两个点到α的距离相等,则 |
已知直线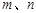 与平面
与平面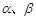 ,给出下列三个命题:
,给出下列三个命题:
①若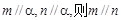 ②若
②若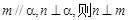
③若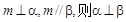 ④
④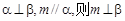
其中真命题的是( )
| A.②③ | B.②③④ | C.②③④ | D.①④ |
如图,在透明塑料制成的长方体 容器内灌进一些水,将容器底面一边
容器内灌进一些水,将容器底面一边 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
①水的部分始终呈棱柱状;
②水面四边形 的面积不改变;
的面积不改变;
③棱 始终与水面
始终与水面 平行;
平行;
④当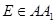 时,
时,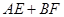 是定值.
是定值.
其中所有正确的命题的序号是( )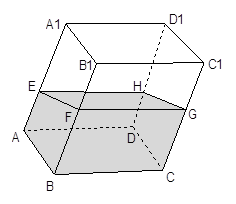
| A.①②③ | B.①③ | C.②④ | D.①③④ |
如图,在空间直角坐标系中有直三棱柱 ,
, ,则直线
,则直线 与直线
与直线 夹角的余弦值为( )
夹角的余弦值为( )
A. | B. | C.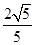 | D. |
如图,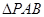 所在的平面
所在的平面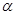 和四边形
和四边形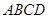 所在的平面
所在的平面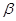 互相垂直,且
互相垂直,且 ,
,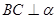 ,
,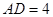 ,
,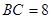 ,
,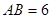 .若
.若 ,则动点
,则动点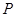 在平面
在平面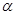 内的轨迹是
内的轨迹是 
| A.椭圆的一部分 | B.线段 | C.双曲线的一部分 | D.以上都不是 |
若直线 ∥平面
∥平面 ,直线
,直线 ,则
,则 与
与 的位置关系是 ( )
的位置关系是 ( )
A. ∥ ∥ | B. 与 与 异面 异面 |
C. 与 与 相交 相交 | D. 与 与 没有公共点 没有公共点 |
已知m、n为两条不同的直线,α、β为两个不同的平面,下列命题中正确的是( )
A.若 | B.若 |
C.若 | D.若 |
 =
= =
= ,则( )
,则( )