题目内容
设数列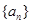 的前
的前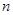 项和为
项和为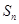 ,
,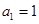 ,且
,且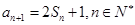 .
.
(Ⅰ)求数列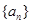 的通项公式;
的通项公式;
(Ⅱ)等差数列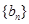 的各项均为正数,其前
的各项均为正数,其前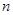 项和为
项和为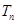 ,且
,且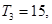 又
又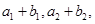
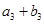 成等比数列,求
成等比数列,求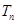 ;
;
(III)求数列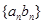 的前
的前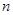 项和
项和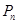 .
.
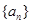 的前
的前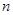 项和为
项和为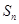 ,
,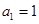 ,且
,且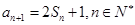 .
.(Ⅰ)求数列
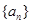 的通项公式;
的通项公式;(Ⅱ)等差数列
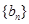 的各项均为正数,其前
的各项均为正数,其前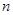 项和为
项和为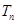 ,且
,且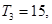 又
又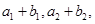
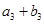 成等比数列,求
成等比数列,求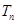 ;
;(III)求数列
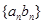 的前
的前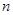 项和
项和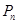 .
.(Ⅰ) .
.
(Ⅱ)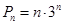 .
.
 .
. (Ⅱ)
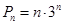 .
.(Ⅰ)当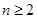 时,
时,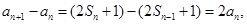 即
即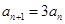 ,
,
再令n=1可得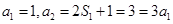 ,从而可知
,从而可知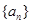 是首项为
是首项为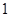 ,公比为
,公比为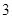 的等比数列.故
的等比数列.故 .
.
(II)在(I)的基础上,根据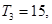 又
又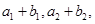
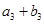 成等差数列,可求出b1和d,再利用等差数列前n项和公式求
成等差数列,可求出b1和d,再利用等差数列前n项和公式求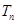 .
.
(III)由于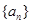 为等比数列,
为等比数列,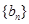 为等差数列,所以数列
为等差数列,所以数列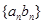 的前
的前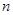 项和
项和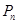 要用错位相减的方法求和.
要用错位相减的方法求和.
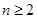 时,
时,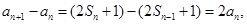 即
即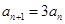 ,
, 再令n=1可得
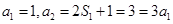 ,从而可知
,从而可知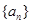 是首项为
是首项为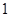 ,公比为
,公比为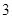 的等比数列.故
的等比数列.故 .
.(II)在(I)的基础上,根据
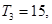 又
又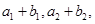
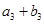 成等差数列,可求出b1和d,再利用等差数列前n项和公式求
成等差数列,可求出b1和d,再利用等差数列前n项和公式求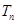 .
.(III)由于
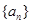 为等比数列,
为等比数列,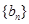 为等差数列,所以数列
为等差数列,所以数列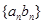 的前
的前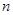 项和
项和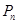 要用错位相减的方法求和.
要用错位相减的方法求和.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
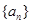 中,已知
中,已知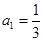 ,
,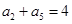 ,
,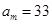 ,则m为______________.
,则m为______________.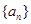 的公差为
的公差为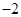 ,且
,且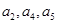 成等比数列,则
成等比数列,则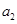 等于 ( )
等于 ( )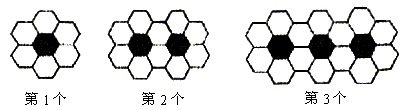
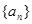 的前
的前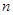 项和为
项和为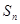 , 且
, 且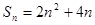 . 设数列
. 设数列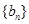 的前
的前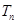 ,且
,且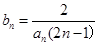 . (1)求
. (1)求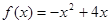 ,对(1)中的数列
,对(1)中的数列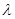 ,使得当
,使得当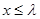 时,
时,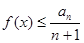 对任意
对任意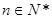 恒成立
恒成立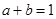 ,
,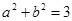 ,
,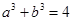 ,
,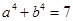 ,
, ,
,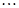 则
则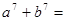 ( )
( )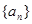 和
和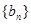 的前n项和分别为
的前n项和分别为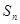 和
和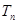 ,对一切自然数n,都有
,对一切自然数n,都有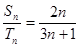 ,则
,则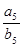 等于 ( )
等于 ( )