题目内容
①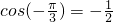 ;②sin(3π+α)=-sinα;③cos(3π+α)=-cosα;④
;②sin(3π+α)=-sinα;③cos(3π+α)=-cosα;④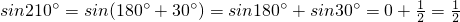 .
.
在以上算式中,正确的是
- A.①②
- B.②③
- C.③④
- D.①④
B
分析:①根据余弦函数为偶函数得到cos(- )=cos
)=cos ,然后利用特殊角的三角函数值求出值,即可做出判断;
,然后利用特殊角的三角函数值求出值,即可做出判断;
②把3π+α变为2π+(π+α),两次利用诱导公式即可得到化简结果,做出判断;
③把3π+α变为2π+(π+α),两次利用诱导公式即可得到化简结果,做出判断;
④把210°变为180°+30°,利用诱导公式及特殊角的三角函数值即可求出值,做出判断.
解答:①cos(- )=cos
)=cos =
= ,本选项错误;
,本选项错误;
②sin(3π+α)=sin[2π+(π+α)]=sin(π+α)=-sinα,本选项正确;
③cos(3π+α)=cos[2π+(π+α)]=cos(π+α)=-cosα,本选项正确;
④sin210°=sin(180°+30°)=-sin30°=- ,本选项错误,
,本选项错误,
则以上算式中,正确的选项是②③.
故选B
点评:此题考查了运用诱导公式化简求值,灵活变换角度,熟练掌握诱导公式是解本题的关键.
分析:①根据余弦函数为偶函数得到cos(-
 )=cos
)=cos ,然后利用特殊角的三角函数值求出值,即可做出判断;
,然后利用特殊角的三角函数值求出值,即可做出判断;②把3π+α变为2π+(π+α),两次利用诱导公式即可得到化简结果,做出判断;
③把3π+α变为2π+(π+α),两次利用诱导公式即可得到化简结果,做出判断;
④把210°变为180°+30°,利用诱导公式及特殊角的三角函数值即可求出值,做出判断.
解答:①cos(-
 )=cos
)=cos =
= ,本选项错误;
,本选项错误;②sin(3π+α)=sin[2π+(π+α)]=sin(π+α)=-sinα,本选项正确;
③cos(3π+α)=cos[2π+(π+α)]=cos(π+α)=-cosα,本选项正确;
④sin210°=sin(180°+30°)=-sin30°=-
 ,本选项错误,
,本选项错误,则以上算式中,正确的选项是②③.
故选B
点评:此题考查了运用诱导公式化简求值,灵活变换角度,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=sin(2x+
)的图象( )
| π |
| 3 |
| A、关于原点对称 | ||
| B、关于y轴对称 | ||
C、关于点(-
| ||
D、关于直线x=
|
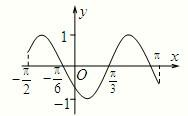 函数y=f(x)在区间[-
函数y=f(x)在区间[-| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(x+
| ||
D、f(x)=sin(x-
|