题目内容
已知定点A(﹣3,0),MN分别为x轴、y轴上的动点(M、N不重合),且AN⊥MN,点P在直线MN上,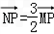 .
.
(1)求动点P的轨迹C的方程;
(2)设点Q是曲线x2+y2﹣8x+15=0上任一点,试探究在轨迹C上是否存在点T?使得点T到点Q的距离最小,若存在,求出该最小距离和点T的坐标,若不存在,说明理由.
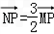 .
.(1)求动点P的轨迹C的方程;
(2)设点Q是曲线x2+y2﹣8x+15=0上任一点,试探究在轨迹C上是否存在点T?使得点T到点Q的距离最小,若存在,求出该最小距离和点T的坐标,若不存在,说明理由.
解:(1)设点M、N的坐标分别为(a,0),(0,b),(a≠0,b≠0),点P的坐标为(x,y),则
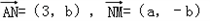 ,
, ,
,
由AN⊥MN得3a﹣b2=0,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(*)
由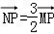 得
得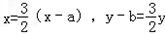
∴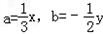 代入(*)得
代入(*)得
y2=4x
∵a≠0,b≠0
∴x≠0,y≠0
∴动点P的轨迹C的方程为y2=4x(x≠0)
(2)曲线x2+y2﹣8x+15=0,即(x﹣4)2+y2=1,是以B(4,0)为圆心,以1为半径的圆,
设 T为轨迹C上任意一点,连接TB,则
|TQ|+|QB|≥|TB|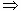 |TQ|≥|TB|﹣1
|TQ|≥|TB|﹣1
∴当|TB|最小时,|TQ|最小.
∵点T在轨迹C上,
设点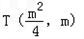 (m≠0)
(m≠0)
∴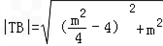 =
=
当m2=8,即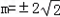 时,|TB|有最小值,
时,|TB|有最小值,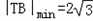
当m2=8时,
∴在轨迹C上是存在点T,其坐标为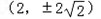 ,使得|TQ|最小,
,使得|TQ|最小,
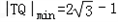 .
.
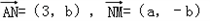 ,
, ,
,由AN⊥MN得3a﹣b2=0,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(*)
由
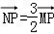 得
得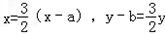
∴
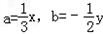 代入(*)得
代入(*)得y2=4x
∵a≠0,b≠0
∴x≠0,y≠0
∴动点P的轨迹C的方程为y2=4x(x≠0)
(2)曲线x2+y2﹣8x+15=0,即(x﹣4)2+y2=1,是以B(4,0)为圆心,以1为半径的圆,
设 T为轨迹C上任意一点,连接TB,则
|TQ|+|QB|≥|TB|
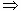 |TQ|≥|TB|﹣1
|TQ|≥|TB|﹣1∴当|TB|最小时,|TQ|最小.
∵点T在轨迹C上,
设点
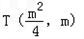 (m≠0)
(m≠0)∴
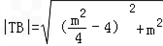 =
=
当m2=8,即
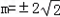 时,|TB|有最小值,
时,|TB|有最小值,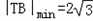
当m2=8时,

∴在轨迹C上是存在点T,其坐标为
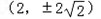 ,使得|TQ|最小,
,使得|TQ|最小,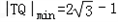 .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目