题目内容
设n∈N﹡且n≥2,若an是(1+x)n展开式中含x2项的系数,则
+
+…+
=
.
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 2(n-1) |
| n |
| 2(n-1) |
| n |
分析:根据二项展开式的通项公式求得x2项的系数,然后利用裂项求和法求出所求即可.
解答:解:在(1+x)n的展开式中,通项公式为Tr+1=
•xr,令r=2,则x2项的系数为an=
=
∴
=
=2(
-
)
∴
+
+…+
=2(1-
+
-
+…+
-
)=2(1-
)=
故答案为:
| C | r n |
| C | 2 n |
| n(n-1) |
| 2 |
∴
| 1 |
| an |
| 2 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
| 2(n-1) |
| n |
故答案为:
| 2(n-1) |
| n |
点评:本题主要考查二项展开式的通项公式,求展开式中某项的系数,以及裂项求和法求和,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
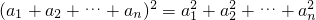 +2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an].
+2[a1(a2+a3+…+an)+a2(a3+a4+…+an)+…+an-1an]. …
… 对一切n∈N*且n≥2恒成立,求实数k的取值范围.
对一切n∈N*且n≥2恒成立,求实数k的取值范围.