题目内容
18.设全集U=R.(Ⅰ)解关于x的不等式|x-1|+a-1>0(a∈R);
(Ⅱ)记A为(Ⅰ)中不等式的解集,集合B={x|sin(![]() )+
)+
![]() cos(
cos(![]() )=0}.若(
)=0}.若(![]() UA)∩B恰有3个元素,求a的取值范围.
UA)∩B恰有3个元素,求a的取值范围.
18.本小题主要考查集合的有关概念,含绝对值的不等式,简单三角函数式的化简和已知三角函数值求角等基础知识,考查简单的分类讨论方法,以及分析问题和推理计算能力.
解:(Ⅰ)由|x-1|+a-1>0,得|x-1|>1-a.
当a>1时,解集是R;
当a≤1时,解集是{x|x<a或x>2-a}.
(Ⅱ)当a>1时,![]() UA=
UA=![]() ;
;
当a≤1时,![]() UA={x|a≤x≤2-a}.
UA={x|a≤x≤2-a}.
因sin(πx-![]() )+
)+![]() cos(πx-
cos(πx-![]() )
)
=2[sin(πx-![]() )cos
)cos![]() +cos(πx-
+cos(πx-![]() )sin
)sin![]() ]=2sinπx,
]=2sinπx,
由sinπx=0,得πx=kπ(k∈Z),即x=k∈Z,所以B=Z.
当(![]() UA)∩B恰有3个元素时,a应满足
UA)∩B恰有3个元素时,a应满足
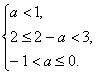
解得-1<a≤0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集U=R,集合M={x|
=
,x∈R},N={x|
≤2,x∈R},则(?UM)∩N等于( )
| x |
| x2-2 |
| x+1 |
| A、{2} |
| B、{x|-1≤x≤3} |
| C、{x|x<2或2<x<3} |
| D、{x|-1≤x<2或2<x≤3} |