Question

设X是一个离散型随机变量，其分布列如下表，试求EX，DX.

X	-1	0	1
P		1-2q	q2

 

 

Answer 1

思路分析：依题意，先应按分布列的性质，求出q的数值后，再计算出EX与DX.

解析：由于离散型随机变量的分布列满足

(1)p_i≥0,i=1,2,3,…;

(2)p₁+p₂+…+p_n+…=1.

故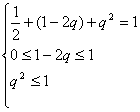

解得   q=1-

故X的分布列为

X	-1	0	1
P

∴EX=(-1)×+0×(-1)+1×()

=-+（-）=1-

DX=［-1-（1-)］²×+（1-）²×（-1）+［1-（1-)］²×()

=（-2）²×+（-1）³+2()=-1