题目内容
设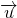 
=（-2，2，5）、
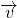=（6，-4，4）分别是平面α，β的法向量，则平面α，β的位置关系是
- A.平行
- B.垂直
- C.相交但不垂直
- D.不能确定
B
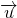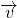分析：先根据向量的坐标运算计算向量与向量的数量积，然后根据数量积为0得到两向量垂直，从而判断出两平面的位置关系．
解答：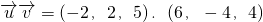
=-2×6+2×（-4）+5×4=0
∴⊥
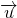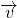
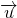∵=（-2，2，5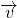）、=（6，-4，4）分别是平面α，β的法向量
∴平面α与平面β垂直
故选B
点评：本题主要考查了向量数量积以及向量垂直的充要条件，同时考查了两平面的位置关系与法向量之间的关系，属于基础题．
分析：先根据向量的坐标运算计算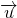向量
与向量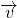的数量积，然后根据数量积为0得到两向量垂直，从而判断出两平面的位置关系．解答：
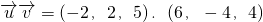=-2×6+2×（-4）+5×4=0∴
⊥∵
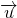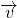
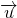=（-2，2，5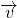）、=（6，-4，4）分别是平面α，β的法向量∴平面α与平面β垂直
故选B
点评：本题主要考查了向量数量积以及向量垂直的充要条件，同时考查了两平面的位置关系与法向量之间的关系，属于基础题．
练习册系列答案
相关题目
