题目内容
为了提高产品的年产量,某企业拟在2010年进行技术改革.经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3-| k | m+1 |
(1)将2010年该产品的利润y万元(利润=销售金额-生产成本-技术改革费用)表示为技术改革费用m万元的函数;
(2)该企业2010年的技术改革费用投入多少万元时,厂家的利润最大?
分析:(1)首先根据题意令m=0代入x=3-
求出常量k,这样就得出了x与m的关系式,然后根据2010年固定收入加再投入资金求出总成本为8+16x,再除以2010的件数就可以得出2010年每件的成本,而每件的销售价格是成本的1.5倍,从而得出了每件产品的销售价格为1.5×
(元),然后用每件的销售单价×销售数量得到总销售额为x•(1.5×
).最后利用利润=销售金额-生产成本-技术改革费用得出利润y的关系式.
(2)根据a+b≥2
当且仅当a=b时取等号的方法求出y的最大值时m的取值即可.
| k |
| m+1 |
| 8+16x |
| x |
| 8+16x |
| x |
(2)根据a+b≥2
| ab |
解答:解:(1)由题意可知,当m=0时,x=1(万件)∴1=3-k,∴k=2,∴x=3-
每件产品的销售价格为1.5×
(元),
∴2010年的利润y=x•[1.5×
]-(8+16x)-m=-[
+(m+1)]+29(元)(m≥0)
(2)∵m≥0,∴
+(m+1)≥2
=8,
∴y≤29-8=21.
当
=m+1,即m=3,ymax=21.
∴该企业2010年的技术改革费用投入3万元时,厂家的利润最大.
| 2 |
| m+1 |
每件产品的销售价格为1.5×
| 8+16x |
| x |
∴2010年的利润y=x•[1.5×
| 8+16x |
| x |
| 16 |
| m+1 |
(2)∵m≥0,∴
| 16 |
| m+1 |
| 16 |
∴y≤29-8=21.
当
| 16 |
| m+1 |
∴该企业2010年的技术改革费用投入3万元时,厂家的利润最大.
点评:本题主要考查学生根据实际问题列出函数解析式的能力,以及求函数最值的问题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
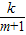 (k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)
(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金) (k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).
(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).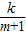 (k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).
(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).