题目内容
在以下关于向量的命题中,不正确的是( )A.若向量a=(x,y),向量b=(-y,x),(xy≠0),则a⊥b
B.平行四边形ABCD是菱形的充要条件是(
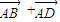 )(
)(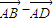 )=0
)=0C.点G是△ABC的重心,则
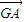 +
+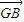 +
+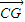 =
=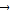
D.△ABC中,
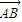 和
和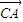 的夹角等于180°-A
的夹角等于180°-A
【答案】分析:A:直接根据向量垂直的条件即可得;
B:要证明ABCD是菱形的充要条件是对角线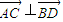 .(
.(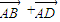 )(
)(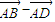 )=0,即证明:
)=0,即证明: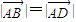 即可;
即可;
C:先判断点G是△ABC的重心,则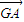 +
+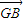 +
+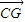 =
=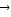 命题是否成立,结合向量的运算法则和几何意义,设G是△ABC的重心,由重心的性质得
命题是否成立,结合向量的运算法则和几何意义,设G是△ABC的重心,由重心的性质得 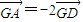 ,得出命题不成立.
,得出命题不成立.
D:根据向量夹角的定义可知其正确性.
解答: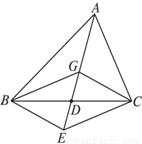 解:A:∵
解:A:∵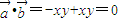 ,∴
,∴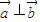 ,故正确;
,故正确;
B:若ABCD是菱形,则: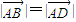 则(
则(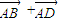 )(
)(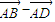 )=0;反之,若(
)=0;反之,若(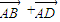 )(
)(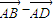 )=0则
)=0则 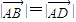 即平行四边形的两邻边相等,则四边形为菱形.故正确;
即平行四边形的两邻边相等,则四边形为菱形.故正确;
C:如图:设G是△ABC的重心,则G是△ABC的三边中线的交点,∴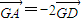 ,
,
又-2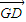 =-(
=-( 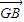 +
+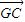 ),∴
),∴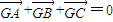 .∴C不成立.
.∴C不成立.
D:根据向量夹角的定义可知:△ABC中,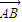 和
和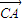 的夹角等于180°-A.故正确.
的夹角等于180°-A.故正确.
故选C.
点评:本题考查向量运算的法则和几何意义,三角形重心的性质,充分条件、必要条件的判断.
B:要证明ABCD是菱形的充要条件是对角线
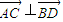 .(
.(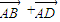 )(
)(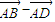 )=0,即证明:
)=0,即证明: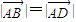 即可;
即可;C:先判断点G是△ABC的重心,则
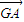 +
+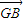 +
+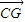 =
=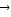 命题是否成立,结合向量的运算法则和几何意义,设G是△ABC的重心,由重心的性质得
命题是否成立,结合向量的运算法则和几何意义,设G是△ABC的重心,由重心的性质得 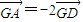 ,得出命题不成立.
,得出命题不成立.D:根据向量夹角的定义可知其正确性.
解答:
 解:A:∵
解:A:∵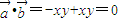 ,∴
,∴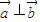 ,故正确;
,故正确;B:若ABCD是菱形,则:
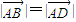 则(
则(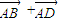 )(
)(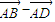 )=0;反之,若(
)=0;反之,若(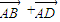 )(
)(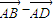 )=0则
)=0则 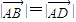 即平行四边形的两邻边相等,则四边形为菱形.故正确;
即平行四边形的两邻边相等,则四边形为菱形.故正确;C:如图:设G是△ABC的重心,则G是△ABC的三边中线的交点,∴
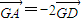 ,
,又-2
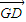 =-(
=-( 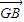 +
+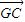 ),∴
),∴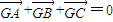 .∴C不成立.
.∴C不成立.D:根据向量夹角的定义可知:△ABC中,
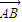 和
和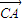 的夹角等于180°-A.故正确.
的夹角等于180°-A.故正确.故选C.
点评:本题考查向量运算的法则和几何意义,三角形重心的性质,充分条件、必要条件的判断.

练习册系列答案
相关题目
在以下关于向量的命题中,不正确的是( )
| A、若向量a=(x,y),向量b=(-y,x),(xy≠0),则a⊥b | ||||||||
B、平行四边形ABCD是菱形的充要条件是(
| ||||||||
C、点G是△ABC的重心,则
| ||||||||
D、△ABC中,
|
在以下关于向量的命题中,不正确的是( )
A、若向量
| ||||||||
B、在△ABC中,
| ||||||||
C、四边形ABCD是菱形的充要条件是
| ||||||||
D、点G是△ABC的重心,则
|
在以下关于向量的命题中,不正确的是( )
A、若向量
| ||||||||
B、△ABC中,有
| ||||||||
C、△ABC中
| ||||||||
D、已知四边形ABCD,则四边形ABCD是菱形的充要条件是
|
 .
. +
+ +
+ =
=
 和
和 的夹角等于180°-A
的夹角等于180°-A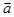 =(x, y),向量
=(x, y),向量 =(-y,x) (xy≠0),则
=(-y,x) (xy≠0),则

 的夹角为角A
的夹角为角A