题目内容
设α表示平面，l，m表示两条不重合的直线，给定下列四个命题
①l∥α，l⊥m⇒m⊥α
②l∥m，l⊥α⇒m⊥α
③l⊥α，l⊥m⇒m∥α
④l⊥α，m⊥α⇒l∥m
其中正确的命题的个数是（ ）
①l∥α，l⊥m⇒m⊥α
②l∥m，l⊥α⇒m⊥α
③l⊥α，l⊥m⇒m∥α
④l⊥α，m⊥α⇒l∥m
其中正确的命题的个数是（ ）
分析：利用线面位置关系的判定、性质，借助于正方体中线面位置关系帮助举例或论证各选项的正误．
解答：解：①如图，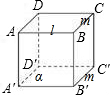
l∥α，l⊥m，m与α可以平行，也可以m在面α内．未必m⊥α ①错
②根据线面垂直的性质：两条平行线中的一条直线与一个平面垂直，那么另一条直线也和这个平面垂直． ②对．
③如图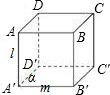
l⊥α，l⊥m，可以m在面α内，未必m∥α． ③错．
④根据线面垂直的性质定理：垂直于同一个平面的两条直线平行，④对
正确的命题的个数是 2
故选B．
l∥α，l⊥m，m与α可以平行，也可以m在面α内．未必m⊥α ①错②根据线面垂直的性质：两条平行线中的一条直线与一个平面垂直，那么另一条直线也和这个平面垂直． ②对．
③如图
l⊥α，l⊥m，可以m在面α内，未必m∥α． ③错．④根据线面垂直的性质定理：垂直于同一个平面的两条直线平行，④对
正确的命题的个数是 2
故选B．
点评：本题考查空间线线、线面位置关系的判定．利用有关的定义、性质、定理来说明命题的正确性，可借助于正方体中线线、线面位置关系举反例说明命题的错误性．
练习册系列答案
相关题目