题目内容
在Rt△ABC中，AB=AC=1.如果一个椭圆通过A，B两点，它的一个焦点为点C，另一个焦点在AB上，则这个椭圆的离心率为( )A.
B.
-1 C.
D.
解析：设另一个焦点为C′，则有
AC+AC′=2a,BC+BC′=2a,
又∵BC=，BC′=1-AC′，
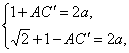∴解得AC′=，a=,
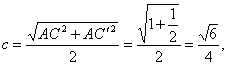
∴离心率e=
,故选A.
答案：A
温馨提示
本题运用椭圆的定义、离心率公式先列出关于某些特征量的方程组，然后通过解方程求出这些特征量，最后求出离心率的值，这是解圆锥曲线问题的常用方法.
练习册系列答案
相关题目
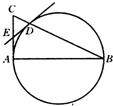15、如图，在Rt△ABC中，∠A=90°，以AB为直径的半圆交BC于D，过D作圆的切线交AC于E．在Rt△ABC中，∠A=90°，|
|=1，则
•
的值为：（ ）
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |