题目内容
已知函数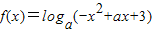 (a>0,且a≠1).
(a>0,且a≠1).(Ⅰ)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围;
(Ⅱ)是否存在这样的实数a,使得函数f(x)在[1,2]上的最大值是2?若存在,求出a的值;若不存在,请说明理由.
【答案】分析:(Ⅰ)由 (a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,知g(x)=-x2+ax+3在[0,2]上恒大于零,由此能求出实数a的取值范围.
(a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,知g(x)=-x2+ax+3在[0,2]上恒大于零,由此能求出实数a的取值范围.
(Ⅱ)由(Ⅰ)知,a ,且a≠1.分别由
,且a≠1.分别由 ,1<a≤2,2<a≤4,a>4四种情况进行讨论,能够推导出存在这样的实数a,使得函数f(x)在[1,2]上的最大值是2,并能求出a的值.
,1<a≤2,2<a≤4,a>4四种情况进行讨论,能够推导出存在这样的实数a,使得函数f(x)在[1,2]上的最大值是2,并能求出a的值.
解答:解:(Ⅰ)∵ (a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,
(a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,
∴g(x)=-x2+ax+3在[0,2]上恒大于零,
∵a>0,∴g(x)的对称轴x= ,
,
①当0< ≤1时,g(x)在[0,2]上的最小值为g(2)=2a-1>0,
≤1时,g(x)在[0,2]上的最小值为g(2)=2a-1>0,
∴ ,且a≠1;
,且a≠1;
②当 时,g(x)在[0,2]上的最小值为g(0)=3>0,成立.
时,g(x)在[0,2]上的最小值为g(0)=3>0,成立.
综上所述,实数a的取值范围是{a|a ,且a≠1}.
,且a≠1}.
(Ⅱ)由(Ⅰ)知,a ,且a≠1.
,且a≠1.
①当 时,f(x)在[1,2]上是增函数,
时,f(x)在[1,2]上是增函数,
f(x)max=f(2)=loga(-4+2a+3)=2,解得a=1,不成立;
②当1<a≤2时,f(x)在[1,2]上是减函数,
f(x)max=f(1)=loga(-1+a+3)=2,解得a=-1不成立,或a=2,成立;
③当2<a≤4时,f(x)在[1,2]上f(x)max=f(a)=loga(-a2+a2+3)=2,解得a= ,成立;
,成立;
④当a>4时,f(x)在[1,2]上是增函数,
f(x)max=f(2)=loga(-4+2a+3)=2,解得a=1,不成立.
综上,a= ,或a=2.
,或a=2.
点评:本题考查复合函数中参数的取值范围的求法,探索是否存在这样的实数a,使得函数f(x)在[1,2]上的最大值是2.综合性强,难度大,对数学思维的要求较高.解题时要认真审题,注意等价转化思想和分类讨论思想的合理运用.
 (a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,知g(x)=-x2+ax+3在[0,2]上恒大于零,由此能求出实数a的取值范围.
(a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,知g(x)=-x2+ax+3在[0,2]上恒大于零,由此能求出实数a的取值范围.(Ⅱ)由(Ⅰ)知,a
 ,且a≠1.分别由
,且a≠1.分别由 ,1<a≤2,2<a≤4,a>4四种情况进行讨论,能够推导出存在这样的实数a,使得函数f(x)在[1,2]上的最大值是2,并能求出a的值.
,1<a≤2,2<a≤4,a>4四种情况进行讨论,能够推导出存在这样的实数a,使得函数f(x)在[1,2]上的最大值是2,并能求出a的值.解答:解:(Ⅰ)∵
 (a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,
(a>0,且a≠1),当x∈[0,2]时,函数f(x)恒有意义,∴g(x)=-x2+ax+3在[0,2]上恒大于零,
∵a>0,∴g(x)的对称轴x=
 ,
,①当0<
 ≤1时,g(x)在[0,2]上的最小值为g(2)=2a-1>0,
≤1时,g(x)在[0,2]上的最小值为g(2)=2a-1>0,∴
 ,且a≠1;
,且a≠1;②当
 时,g(x)在[0,2]上的最小值为g(0)=3>0,成立.
时,g(x)在[0,2]上的最小值为g(0)=3>0,成立.综上所述,实数a的取值范围是{a|a
 ,且a≠1}.
,且a≠1}.(Ⅱ)由(Ⅰ)知,a
 ,且a≠1.
,且a≠1.①当
 时,f(x)在[1,2]上是增函数,
时,f(x)在[1,2]上是增函数,f(x)max=f(2)=loga(-4+2a+3)=2,解得a=1,不成立;
②当1<a≤2时,f(x)在[1,2]上是减函数,
f(x)max=f(1)=loga(-1+a+3)=2,解得a=-1不成立,或a=2,成立;
③当2<a≤4时,f(x)在[1,2]上f(x)max=f(a)=loga(-a2+a2+3)=2,解得a=
 ,成立;
,成立;④当a>4时,f(x)在[1,2]上是增函数,
f(x)max=f(2)=loga(-4+2a+3)=2,解得a=1,不成立.
综上,a=
 ,或a=2.
,或a=2.点评:本题考查复合函数中参数的取值范围的求法,探索是否存在这样的实数a,使得函数f(x)在[1,2]上的最大值是2.综合性强,难度大,对数学思维的要求较高.解题时要认真审题,注意等价转化思想和分类讨论思想的合理运用.

练习册系列答案
相关题目
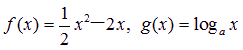 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果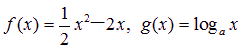 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果 (a>0,且a≠1)
(a>0,且a≠1)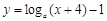 (a > 0,且
(a > 0,且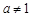 )的图象恒过定点A,若点A在直线
)的图象恒过定点A,若点A在直线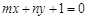 上,其中
上,其中 ,
,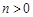 ,则
,则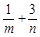 的最小值为__________.
的最小值为__________.