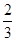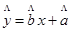题目内容
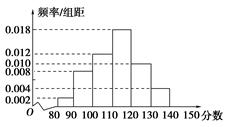
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6.
(1)估计所抽取的数学成绩的众数;
(2)用分层抽样的方法在成绩为 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在 恰有1人的概率.
恰有1人的概率.

 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6.(1)估计所抽取的数学成绩的众数;
(2)用分层抽样的方法在成绩为
 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在 恰有1人的概率.
恰有1人的概率.
(1)75;(2)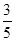
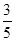
试题分析:(1)由直方图估计所抽取的数学成绩的众数,概率最大数学成绩的是在70-80之间,所以众数的估计值为
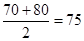 .
.(2)由于其中成绩在
 的学生人数为6,又在
的学生人数为6,又在 间的频率为0.12.所以总人数为50.由于成绩为
间的频率为0.12.所以总人数为50.由于成绩为 和
和 这两组的频率分别是0.24,0.16,所以这两组的抽取的人数分别为12,8人. 用分层抽样的方法这两组中共抽取5个学生,所以这两组分别抽取了3,2人. 从这5个学生中任取2人进行点评共有10种情况.其中分数在
这两组的频率分别是0.24,0.16,所以这两组的抽取的人数分别为12,8人. 用分层抽样的方法这两组中共抽取5个学生,所以这两组分别抽取了3,2人. 从这5个学生中任取2人进行点评共有10种情况.其中分数在 恰有1人的共有6种.所以即可求得结论.
恰有1人的共有6种.所以即可求得结论.(1)由频率分布直方图可知:样本的众数为75. 3分
(2)由频率分布直方图可得:第三组
 的频率:
的频率: ,
,所以
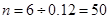 , 4分
, 4分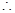 第四组
第四组 的频数:
的频数: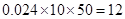 ;
;第五组
 的频数:
的频数: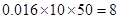 ;
;用分层抽样的方法抽取5份得:
第四组
 抽取:
抽取: ;第五组
;第五组 抽取:
抽取: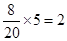 . 7分
. 7分记抽到第四组
 的三位同学为
的三位同学为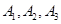 ,抽到第五组
,抽到第五组 的两位同学为
的两位同学为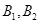
则从5个同学中任取2人的基本事件有:
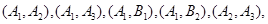
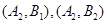 ,
, ,共10种.
,共10种.其中分数在
 恰有1人有:
恰有1人有: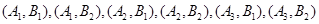 ,共6种.
,共6种. 所求概率:
所求概率: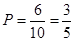 . 12分
. 12分
练习册系列答案
相关题目

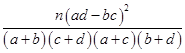 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)
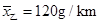 .
.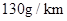 的概率是多少?
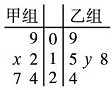
的概率是多少?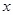 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.