题目内容
已知函数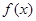 的导数
的导数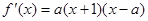 ,若
,若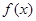 在
在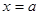 处取得极大值,则
处取得极大值,则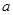 的取值范围是 .
的取值范围是 .
【答案】
(-1,0)
【解析】
试题分析:讨论a的正负,以及a与-1的大小,分别判定在x=a处的导数符号,从而确定是否在x=a处取到极大值,从而求出所求.解:当a>0时,当-1<x<a时,f'(x)<0,当x>a时,f'(x)>0,则f(x)在x=a处取到极小值,不符合题意;当a=0时,函数f(x)无极值,不符合题意;当-1<a<0时,当-1<x<a时,f'(x)>0,当x>a时,f'(x)<0,则f(x)在x=a处取到极大值,符合题意;当a=-1时,f'(x)≤0,,函数f(x)无极值,不符合题意;当a<-1时,当x<a时,f'(x)<0,当a<x<-1时,f'(x)>0,则f(x)在x=a处取到极小值,不符合题意;综上所述-1<a<0,故填写(-1,0)
考点:导数来求解函数极值
点评:解决的关键是根据极值的概念来得到参数a的符号的判定,以及范围的求解,属于基础题。

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 的导数
的导数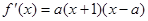 ,若
,若 处取得极大值,则
处取得极大值,则 的取值范围是 .
的取值范围是 .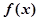 的导数
的导数 ,若
,若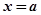 处取到极大值,则实数
处取到极大值,则实数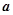 的取值范围是 ▲ .
的取值范围是 ▲ . 的导数
的导数 ,若
,若 处取到极大值,则
处取到极大值,则 的取值范围是( )
的取值范围是( ) B.
B.
 C.
C.
 D.
D.
