题目内容
 如图,设曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴y轴所围成的三角形面积为S(t),求:
如图,设曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴y轴所围成的三角形面积为S(t),求:(1)切线l的方程;
(2)求证S(t)≤
| 2 | e |
分析:(1)先求切线斜率,进而可求切线方程;
(2)根据曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴y轴所围成的三角形面积为S(t),表示出S(t),再用导数法求解.
(2)根据曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴y轴所围成的三角形面积为S(t),表示出S(t),再用导数法求解.
解答:解:(1)∵f′(x)=(e-x)′=-e-x,∴切线l的斜率为-e-t
故切线l的方程为y-e-t=-e-t(x-t),即e-tx+y-e-t(t+1)=0
(2)证明:令y=0得x=t+1,又令x=0得y=e-t(t+1),
∴S(t)=
(t+1)•e-t(t+1)=
(t+1)2e-t
从而S′(t)=
e-t(1-t)(1+t).
∵当t∈(0,1)时,S′(t)>0,当t∈(1,+∞)时,S′(t)<0,
∴S(t)的最大值为S(1)=
,即S(t)≤
故切线l的方程为y-e-t=-e-t(x-t),即e-tx+y-e-t(t+1)=0
(2)证明:令y=0得x=t+1,又令x=0得y=e-t(t+1),
∴S(t)=
| 1 |
| 2 |
| 1 |
| 2 |
从而S′(t)=
| 1 |
| 2 |
∵当t∈(0,1)时,S′(t)>0,当t∈(1,+∞)时,S′(t)<0,
∴S(t)的最大值为S(1)=
| 2 |
| e |
| 2 |
| e |
点评:应用导数法求函数的最值,并结合函数图象,可快速获解,也充分体现了求导法在证明不等式中的优越性.

练习册系列答案
相关题目
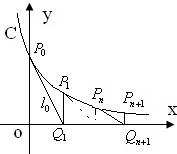 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
 ,N=
,N= ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程. (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长.
(t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长. ≥2y+3.
≥2y+3. 如图,设曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴y轴所围成的三角形面积为S(t),求:
如图,设曲线y=e-x(x≥0)在点M(t,e-t)处的切线l与x轴y轴所围成的三角形面积为S(t),求: .
.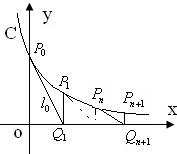 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).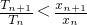 (n∈N+).
(n∈N+).