题目内容
(14分)已知![]() 是实数,函数
是实数,函数![]()
(I)若![]() ,求
,求![]() 的值及曲线
的值及曲线![]() 在点(
在点(![]() )处的切线方程;
)处的切线方程;
(Ⅱ)求![]() 在区间[1,4]上的最大值。
在区间[1,4]上的最大值。
解析:(I)![]() 由
由![]() 得
得![]()
于是![]() 故
故![]()
![]() 切线方程为
切线方程为![]() ,即
,即![]()
(Ⅱ)令![]() ,解得
,解得![]()
①当![]() 时,即
时,即![]() 时,在
时,在![]() 内,
内,![]() ,于是
,于是![]() 在[1,4]内为增函数。从而
在[1,4]内为增函数。从而![]()
②当![]() ,即
,即![]() ,在
,在![]() 内,
内,![]() ,于是
,于是![]() 在[1,4]内为减函数,从而
在[1,4]内为减函数,从而![]()
③当![]() 时,
时,![]() 在
在![]() 内递减,在
内递减,在![]() 内递增,故
内递增,故![]() 在[1,4]上的最大值为
在[1,4]上的最大值为![]() 与
与![]() 的较大者。
的较大者。
由![]() ,得
,得![]() ,故当
,故当![]() 时,
时,![]()
当![]() 时,
时,![]()

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
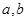 是实数,函数
是实数,函数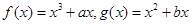 ,
,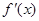 和
和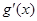 ,分别是
,分别是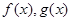 的导函数,若
的导函数,若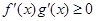 在区间
在区间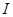 上恒成立,则称
上恒成立,则称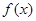 和
和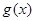 在区间
在区间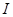 上单调性一致.
上单调性一致.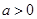 ,若函数
,若函数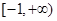 上单调性一致,求实数
上单调性一致,求实数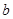 的取值范围;
的取值范围;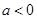 且
且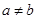 ,若函数
,若函数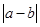 的最大值.
的最大值.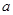 是实数,函数
是实数,函数 。
。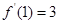 ,求
,求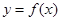 在点
在点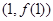 处的切线方程;
处的切线方程;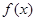 在区间
在区间 上的最大值。
上的最大值。 是实数,函数
是实数,函数 .
.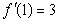 ,求
,求 在点
在点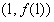 处的切线方程;
处的切线方程;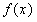 在区间
在区间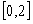 上的最大值.
上的最大值.