题目内容
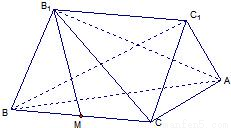
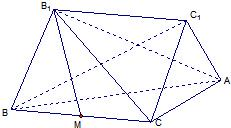 如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°
如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°①求异面直线AB1与BC1所成的角.
②若二面角A-BB1-C的大小为30°,求三棱锥C1-ABC的体积.
③在②的条件下,求直线AB1与平面BCC1B1所成角正切值.
分析:(1)观察图形,易得AC⊥平面B1BCC1,又∵BC1⊥AB1,∴AB1与BC1成900的角.
(2)根据二面角的大小,将其转化成对应的平面角,进而可知:AC=1,则体积也可以求得了.
(3)本题递进式的,在②的条件下,直线AB1与平面BCC1B1所成角即为∠AB1C.
(2)根据二面角的大小,将其转化成对应的平面角,进而可知:AC=1,则体积也可以求得了.
(3)本题递进式的,在②的条件下,直线AB1与平面BCC1B1所成角即为∠AB1C.
解答:解:(1)AC⊥平面B1BCC1,
由于四边形BCC1B1为菱形∴BC1⊥B1C∴BC1⊥AB1
∴AB1与BC1成900的角
(2)取BB1的中点D,连CD,则CD⊥BB1
∴AD⊥BB1∴∠ADC为二面角A-BB1-C的平面角即∠ADC=30°
∴AC=1∴VC1-ABC=VA-BCC1=
S△BCC1•AC=
(3)∠AB1C为直线AB1与平面BCC1B1所成的角,其正切值为
由于四边形BCC1B1为菱形∴BC1⊥B1C∴BC1⊥AB1
∴AB1与BC1成900的角
(2)取BB1的中点D,连CD,则CD⊥BB1
∴AD⊥BB1∴∠ADC为二面角A-BB1-C的平面角即∠ADC=30°
∴AC=1∴VC1-ABC=VA-BCC1=
| 1 |
| 3 |
| ||
| 3 |
(3)∠AB1C为直线AB1与平面BCC1B1所成的角,其正切值为
| 1 |
| 2 |
点评:本小题主要考查空间线面关系、面面关系、二面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为
如图,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为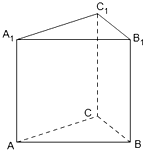 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.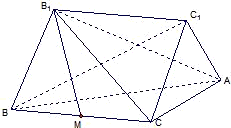 如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°
如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°