题目内容
已知双曲线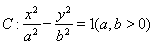 的一条渐近线方程是
的一条渐近线方程是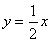 ,它的一个焦点在抛物线
,它的一个焦点在抛物线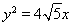 的准线上,点
的准线上,点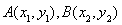 是双曲线
是双曲线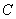 右支上相异两点,且满足
右支上相异两点,且满足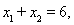
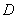 为线段
为线段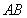 的中点,直线
的中点,直线 的斜率为
的斜率为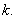
(1)求双曲线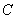 的方程;
的方程;
(2)用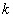 表示点
表示点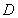 的坐标;
的坐标;
(3)若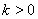 ,
, 的中垂线交
的中垂线交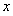 轴于点
轴于点 ,直线
,直线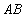 交
交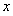 轴于点
轴于点 ,求
,求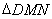 的面积的取值范围.
的面积的取值范围.
【答案】
(1)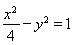 ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:(1)求双曲线的标准方程只需找到两个关于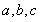 的两个等式,通过解方程即可得到
的两个等式,通过解方程即可得到 的值,从而得到双曲线方程.
的值,从而得到双曲线方程.
(2)由直线AB的方程与双曲线方程联立,消去y可得关于x的一个一元二次方程,判别式必须满足大于零,再由韦达定理可表示出点D的坐标,又根据 即可用k表示点D的纵坐标.从而可求出点D的坐标.
即可用k表示点D的纵坐标.从而可求出点D的坐标.
(3) 的中垂线交
的中垂线交 轴于点
轴于点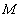 ,直线
,直线 交
交 轴于点
轴于点 求
求 的面积.通过直线AB可以求出点N的坐标,又由线段AB的中垂线及中点D的坐标,可以写出中垂线的方程,再令y=0,即可求出点M.以MN长为底边,高为点D的纵坐标,即可求出面积的表达式.再用最值的求法可得结论.
的面积.通过直线AB可以求出点N的坐标,又由线段AB的中垂线及中点D的坐标,可以写出中垂线的方程,再令y=0,即可求出点M.以MN长为底边,高为点D的纵坐标,即可求出面积的表达式.再用最值的求法可得结论.
试题解析:(1)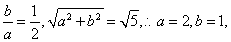
 双曲线
双曲线 的方程为
的方程为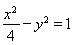 ;
;
(2)方法一:
设直线 的方程为
的方程为 代入方程
代入方程 得
得
 当
当 时记两个实数根为
时记两个实数根为
则

∴ 的方程为
的方程为
 把
把 代入得
代入得
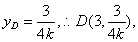
下求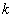 的取值范围:法一:由
的取值范围:法一:由 得
得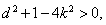 即
即
而 所以
所以 化简得
化简得
法二:在 中令
中令 得
得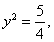

即 所以
所以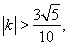
再结合 得
得 ;
;
方法二: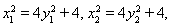 两式相减得
两式相减得

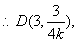
(3)由(2)可知方程
 中令
中令 得
得
设点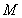 的坐标为
的坐标为 由
由 得
得
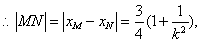
∴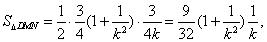
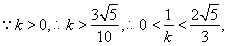

考点:1.双曲线的性质.2.直线与双曲线的位置关系.3.三角形的面积的求法.4.最值的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2 分别是双曲线
分别是双曲线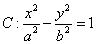
 的左,右焦点。过点
的左,右焦点。过点 与双曲线的一条渐
与双曲线的一条渐 ,且
,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) (B)
(B) 
 (D)
(D)
