Question

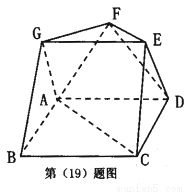
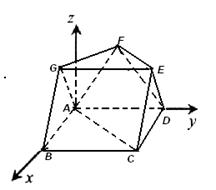
如图，在多面体ABCDEFG中，四边形ABCD是边长为2的正方形，平面ABG、平面ADF、平面CDE都与平面ABCD垂直，且ΔABG, ΔADF, ΔCDE都是正三角形.

(I)求证：AC// EF ；

(II) 求多面体ABCDEFG的体积.

 

Answer 1

【答案】

(Ⅰ) 证明：方法一，如图，分别取AD、CD的中点P、Q，连接FP，EQ.

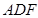∵△和△是为2的正三角形，

∴FP⊥AD,EQ⊥CD,且FP=EQ=.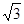

又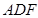∵平面、平面都与平面垂直，

∴FP⊥平面, EQ⊥平面,∴FP∥QE且FP=EQ，

∴四边形EQPF是平行四边形，∴EF∥PQ.　　 ……………………….……..４分

∵ PQ是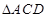的中位线，∴PQ∥AC,

∴ EF∥AC　………………………..……..6分

方法二，以A点作为坐标原点，以AB所在直线为x轴，以AD所在直线为y轴，过点A垂直于平面的直线为z轴，建立空间直角坐标系，如图所示．

根据题意可得，A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),E(1,2,)，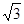

F(0,1,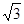)，G(1,0,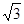). …………………………………………..………………..４分

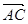∴=（2，2，0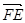），=(1，1，0)，则=，

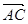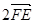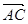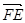∴∥，即有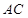∥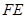……………………………………………..……..6分

(Ⅱ)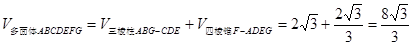

【解析】略