题目内容
(5分)(2011•重庆)若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是 .
2﹣log23
解析试题分析:由基本不等式得2a+2b≥ ,可求出2a+b的范围,
,可求出2a+b的范围,
再由2a+2b+2c=2a+b+c=2a+b2c=2a+b+2c,2c可用2a+b表达,利用不等式的性质求范围即可.
解:由基本不等式得2a+2b≥ ,即2a+b≥
,即2a+b≥ ,所以2a+b≥4,
,所以2a+b≥4,
令t=2a+b,由2a+2b+2c=2a+b+c可得2a+b+2c=2a+b2c,所以2c=
因为t≥4,所以 ,即
,即 ,所以
,所以
故答案为:2﹣log23
点评:本题考查指数的运算法则,基本不等式求最值、不等式的性质等问题,综合性较强.

练习册系列答案
相关题目
△ABC满足 ,∠BAC=30°,设M是△ABC内的一点(不在边界上),定义f(M)=(x,y,z),其中
,∠BAC=30°,设M是△ABC内的一点(不在边界上),定义f(M)=(x,y,z),其中 分别表示△MBC,△MCA,△MAB的面积,若
分别表示△MBC,△MCA,△MAB的面积,若 ,则
,则 的最小值为__________________
的最小值为__________________
若 ,则下列不等式成立的是
,则下列不等式成立的是
A. | B. |
C. | D. |
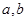 满足
满足 ,则
,则 的取值范围是________________.
的取值范围是________________. ,则△ABC面积S的取值范围是 .
,则△ABC面积S的取值范围是 . 的最小值为_________.
的最小值为_________. ,则
,则 的最小值为_____ 。
的最小值为_____ 。 均为正实数,且
均为正实数,且 ,则
,则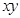 的最小值为__________;
的最小值为__________;