题目内容
设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球2分,取出蓝球得3分.(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和.,求ξ分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若
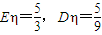 ,求a:b:c.
,求a:b:c.
【答案】分析:(1)ξ的可能取值有:2,3,4,5,6,求出相应的概率可得所求ξ的分布列;
(2)先列出η的分布列,再利用η的数学期望和方差公式,即可得到结论.
解答:解:(1)由题意得ξ=2,3,4,5,6,
P(ξ=2)=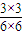 =
= ;P(ξ=3)=
;P(ξ=3)=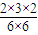 =
= ;P(ξ=4)=
;P(ξ=4)=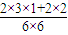 =
=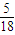 ;
;
P(ξ=5)=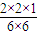 =
= ;P(ξ=6)=
;P(ξ=6)=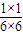 =
=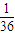 .
.
故所求ξ的分布列为
(2)由题意知η的分布列为
Eη=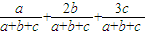 =
=
Dη=(1- )2
)2 +(2-
+(2- )2
)2 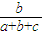 +(3-
+(3- )2
)2 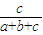 =
= .
.
得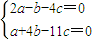 ,
,
解得a=3c,b=2c,
故a:b:c=3:2:1.
点评:本题主要考查随机事件的概率和随机变量的分布列、数学期望等概念,同时考查抽象概括、运算能力,属于中档题.
(2)先列出η的分布列,再利用η的数学期望和方差公式,即可得到结论.
解答:解:(1)由题意得ξ=2,3,4,5,6,
P(ξ=2)=
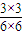 =
= ;P(ξ=3)=
;P(ξ=3)=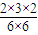 =
= ;P(ξ=4)=
;P(ξ=4)=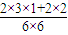 =
=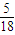 ;
;P(ξ=5)=
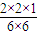 =
= ;P(ξ=6)=
;P(ξ=6)=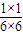 =
=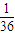 .
.故所求ξ的分布列为
| ξ | 2 | 3 | 4 | 5 | 6 |
| P |  |  | 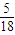 |  | 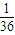 |
| η | 1 | 2 | 3 |
| P | 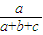 | 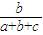 | 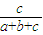 |
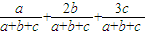 =
=
Dη=(1-
 )2
)2 +(2-
+(2- )2
)2 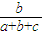 +(3-
+(3- )2
)2 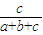 =
= .
.得
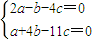 ,
,解得a=3c,b=2c,
故a:b:c=3:2:1.
点评:本题主要考查随机事件的概率和随机变量的分布列、数学期望等概念,同时考查抽象概括、运算能力,属于中档题.

练习册系列答案
相关题目