题目内容
已知等差数列 的首项为
的首项为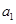 ,公差为
,公差为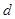 ,其前
,其前 项和为
项和为 ,若直线
,若直线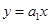 与圆
与圆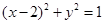 的两个交点关于直线
的两个交点关于直线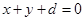 对称,则
对称,则 =
=

解析试题分析:由于直线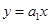 与圆
与圆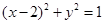 的两个交点关于直线
的两个交点关于直线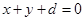 对称,则说明交点所在的直线的斜率为1,且中点在对称轴
对称,则说明交点所在的直线的斜率为1,且中点在对称轴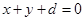 上,那么可知
上,那么可知 联立方程组可知
联立方程组可知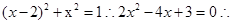 交点的中点坐标为(2,2)满足
交点的中点坐标为(2,2)满足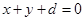 ,得到d=-4,因此可知数列的前n项和为
,得到d=-4,因此可知数列的前n项和为 。
。
考点:数列,直线与圆
点评:解决的关键是利用直线与圆的对称性以及等差数列的公式来求解,属于基础题。

练习册系列答案
相关题目
题目内容
已知等差数列 的首项为
的首项为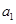 ,公差为
,公差为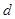 ,其前
,其前 项和为
项和为 ,若直线
,若直线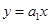 与圆
与圆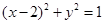 的两个交点关于直线
的两个交点关于直线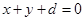 对称,则
对称,则 =
=

解析试题分析:由于直线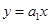 与圆
与圆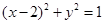 的两个交点关于直线
的两个交点关于直线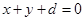 对称,则说明交点所在的直线的斜率为1,且中点在对称轴
对称,则说明交点所在的直线的斜率为1,且中点在对称轴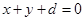 上,那么可知
上,那么可知 联立方程组可知
联立方程组可知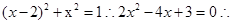 交点的中点坐标为(2,2)满足
交点的中点坐标为(2,2)满足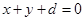 ,得到d=-4,因此可知数列的前n项和为
,得到d=-4,因此可知数列的前n项和为 。
。
考点:数列,直线与圆
点评:解决的关键是利用直线与圆的对称性以及等差数列的公式来求解,属于基础题。
