题目内容
已知点A（4，6），点P是双曲线C：
上的一个动点，点F是双曲线C的右焦点，则PA+PF的最小值为 ．
【答案】分析：由题意可得满足条件的点P在右支上，设左焦点为F′，由双曲线的定义可得PF′-PF=2a，故PA+PF=PA+PF′-2a≥AF′-2a，从而得到结论．
解答：解：由双曲线的方程可得 a=1，b=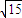
，∴c=4，点F （4，0）．
由题意可得满足条件的点P在右支上，
设左焦点为F′，由双曲线的定义可得 PF′-PF=2a，∴PF=PF′-2a，
∴PA+PF=PA+PF′-2a≥AF′-2a=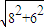
-2=8，
故答案为 8．
点评：本题考查双曲线的定义和标准方程，以及双曲线的简单性质的应用，得出PA+PF=PA+PF′-2a≥AF′-2a，是解题的关键．
解答：解：由双曲线的方程可得 a=1，b=
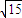，∴c=4，点F （4，0）．由题意可得满足条件的点P在右支上，
设左焦点为F′，由双曲线的定义可得 PF′-PF=2a，∴PF=PF′-2a，
∴PA+PF=PA+PF′-2a≥AF′-2a=
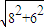-2=8，故答案为 8．
点评：本题考查双曲线的定义和标准方程，以及双曲线的简单性质的应用，得出PA+PF=PA+PF′-2a≥AF′-2a，是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
上的一个动点，点F是双曲线C的右焦点，则PA+PF的最小值为 ．