题目内容
设0<a<b<1,P=log
,Q=
(log
a+log
b),M=
log
(a+b),则P,Q,M从小到大顺序为
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
M<P<Q
M<P<Q
.分析:由已知可得:Q=
log
(ab)=log
,M=log
,P=log
.只要比较
、
、
的大小,再利用函数y=log
x在(0,+∞)上的单调性即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ab |
| 1 |
| 2 |
| a+b |
| 1 |
| 2 |
| a+b |
| 2 |
| ab |
| a+b |
| a+b |
| 2 |
| 1 |
| 2 |
解答:解:由已知可得:Q=
log
(ab)=log
,M=log
,P=log
.
∵0<a<b<1,
∴0<
<
<2,
∴a+b<2
,
∴
<
,
又
>
,
∴
>
>
,
∵函数y=log
x在(0,+∞)上的单调递减,
∴log
<log
<log
,
∴M<P<Q.
故答案为M<P<Q.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ab |
| 1 |
| 2 |
| a+b |
| 1 |
| 2 |
| a+b |
| 2 |
∵0<a<b<1,
∴0<
| a+b |
| 2 |
∴a+b<2
| a+b |
∴
| a+b |
| 2 |
| a+b |
又
| a+b |
| 2 |
| ab |
∴
| a+b |
| a+b |
| 2 |
| ab |
∵函数y=log
| 1 |
| 2 |
∴log
| 1 |
| 2 |
| a+b |
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |
| a b |
∴M<P<Q.
故答案为M<P<Q.
点评:本题考查了基本不等式的性质、对数函数的单调性等基础知识与基本技能方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(
杭州学军中学模拟)设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)等于[
]|
A . |
B .1-p |
C .1-2p |
D .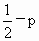 |
 B.1-
B.1- C.1-2
C.1-2