题目内容
已知在各项不为零的数列{an}中,a1=1,anan-1+an-an-1=0(n≥2,n∈N+)
(I)求数列{an}的通项;
(Ⅱ)若数列{bn}满足bn=anan+1,数列{bn}的前n项和为Sn,求
Sn.
(I)求数列{an}的通项;
(Ⅱ)若数列{bn}满足bn=anan+1,数列{bn}的前n项和为Sn,求
| lim |
| n→∞ |
(Ⅰ)依题意,an≠0,故可将anan-1+an-an-1=0(n≥2)整理得:
-
=1(n≥2)
所以
=1+1×(n-1)=n即an=
n=1,上式也成立,所以an=
(Ⅱ)∵bn=anan+1
∴bn=
×
=
=
-
∴Sn=b1+b2+b3++bn=(
-
)+(
-
)+(
-
)++(
-
)=1-
=
∴
Sn=
=1
| 1 |
| an |
| 1 |
| an-1 |
所以
| 1 |
| an |
| 1 |
| n |
n=1,上式也成立,所以an=
| 1 |
| n |
(Ⅱ)∵bn=anan+1
∴bn=
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=b1+b2+b3++bn=(
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| n |
| n+1 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
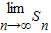 .
.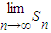 .
.