题目内容
已知A、B、C为 的三个内角且向量
的三个内角且向量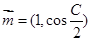 与
与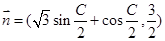 共线.
共线.
(Ⅰ)求角C的大小;
(Ⅱ)设角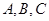 的对边分别是
的对边分别是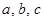 ,且满足
,且满足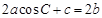 ,试判断
,试判断
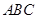 的形状.
的形状.
【答案】
(Ⅰ)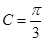 ;(Ⅱ)等边三角形.
;(Ⅱ)等边三角形.
【解析】
试题分析:(Ⅰ)利用共线向量的坐标运算,二倍角公式,辅助角公式变形求得;(Ⅱ)根据余弦定理及已知条件求出边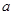 、
、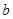 的关系,再结合
的关系,再结合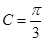 判断出结论.
判断出结论.
试题解析:(Ⅰ)∵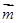 与
与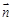 共线,
共线,
∴ 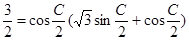
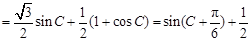 3分
3分
得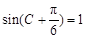 ,
,
∴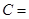
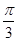 .
6分
.
6分
(Ⅱ)方法1:由已知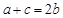 (1)
(1)
根据余弦定理可得: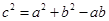 (2)
8分
(2)
8分
(1)、(2)联立解得: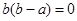 ,
,
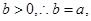 又.
又. 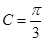 ,所以△
,所以△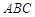 为等边三角形,
12分
为等边三角形,
12分
方法2:
由正弦定理得:
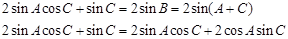 ,
,
∴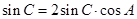 ,
10分
,
10分
∴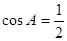 ,
∴在△
,
∴在△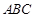 中 ∠
中 ∠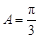
又. 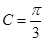 ,
所以 △
,
所以 △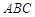 为等边三角形,
12分
为等边三角形,
12分
方法3:由(Ⅰ)知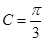 ,又由题设得:
,又由题设得: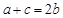 ,
,
在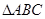 中根据射影定理得:
中根据射影定理得: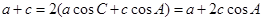 , 10分
, 10分
 ,
,
又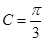 ,
所以 △
,
所以 △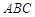 为等边三角形,
12分
为等边三角形,
12分
考点:共线向量的坐标运算,二倍角公式,余弦定理,正弦定理.

练习册系列答案
相关题目
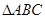 的三个内角,他们的对边分别为a、b、c,且
的三个内角,他们的对边分别为a、b、c,且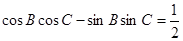 。
。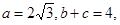 求bc的值,并求
求bc的值,并求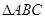 的三个内角且向量
的三个内角且向量 共线。
共线。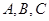 的对边分别是
的对边分别是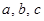 ,且满足
,且满足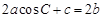 ,试判断
,试判断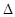
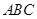 的形状.
的形状.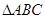 的三个内角且向量
的三个内角且向量 共线。
共线。 的对边分别是
的对边分别是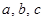 ,且满足
,且满足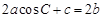 ,试判断
,试判断
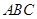 的形状.
的形状.